Симметричные звезды – Если бы у знаменитостей были симметричные лица

Соединение фаз потребителей электроэнергии в звезду

Схема соединения фаз электроприемников «звезда» получила очень широкое распространение в электроэнергетике. Принципиальная схема соединения звездой показана ниже:

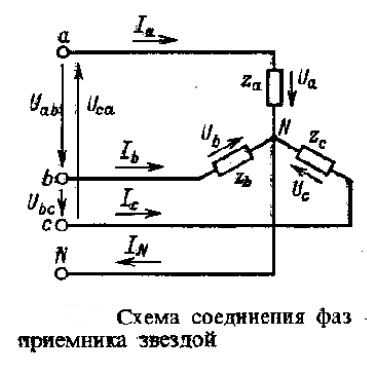
Из схемы видно, что фазные напряжения приемника U_a, U_b, U_c не равны линейным напряжениям U_ab, U_bc, U_ca. Если применить к контурам aNba, bNcb, cNac второй закон Кирхгофа получим соотношение для фазных и линейных напряжений:

Если сопротивления нейтрального провода и линейных проводов не учитывать, то можно предположить, что напряжение на клеммах генератора и электроприемника равны. Вследствие указанного равенства векторные диаграммы для источника и приемника электрической энергии будут одинаковы.

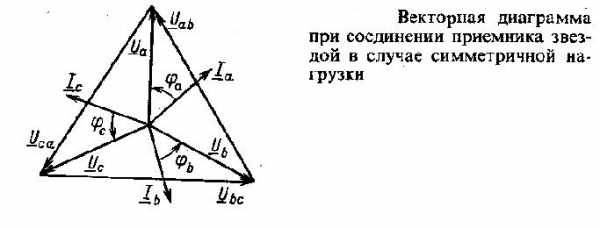
Фазные и линейные напряжения приемника, как и источника, будут образовывать две симметричные системы напряжений. Соответственно между фазными и линейными значениями напряжений будет существовать определенная зависимость:

Далее будет показано, что соотношение (2) будет справедливо лишь при определенных условиях, а также в случае отсутствия нулевого провода, то есть в трехпроводной сети.

Исходя из указанного выше соотношения (2) можно сделать вывод, что соединение звездой лучше применять в случае, когда каждая фаза трехфазного электроприемника или однофазные приемники рассчитаны на напряжение в раз меньше, чем номинальное линейное напряжение сети.

Также из схемы соединения звезда (смотри схему выше) видно, что при соединении приемников звездой фазные токи будут равны линейным:

Применив первый закон Кирхгофа можно получить соотношение между токами при соединении электроприемников звездой:

Зная фазные токи с помощью формулы (4) можно вычислить ток нейтрального провода I_N. В случае отсутствия нейтрального провода справедливо будет выражение:

Симметричная нагрузка при соединении приемников звездой

Нагрузка считается симметричной тогда, когда реактивные и активные сопротивления каждой фазы будут равны, то есть выполняется равенство:

Условие симметричности также может быть выражено через комплексные сопротивления Z_a = Z_b = Z_c.

Симметричная нагрузка в сети возникает при подключении трехфазных электроприемников. Будем считать, что данная система имеет нейтральный провод.

В отношении любой из фаз при симметричной нагрузке будут справедливы все формулы, полученные для однофазной сети, например для фазы А:

Так как в четырехпроводной цепи U_a = U_b = U_c = U_л /  , то при симметричной нагрузке:

Векторная диаграмма при симметричной активно-индуктивной нагрузке приведена выше. Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке образуется симметричная система токов, поэтому ток в нейтральном проводе будет равен I

N = I_a + I_b + I_c = 0.

Отсюда можно сделать вывод, что при симметричной нагрузке отключение нейтрального провода не приведет к серьезным нарушениям работы электроприемников, то есть не произойдет изменение фазных напряжений, углов сдвига, токов, мощностей.

Из сказанного выше следует, что при симметричной нагрузке в нейтральном проводе нет необходимости, и довольно часто в симметричных системах нейтральный провод не применяется.

Мощность трехфазного приемника электрической энергии при симметричной нагрузке можно выразить формулами:

Как правило, для трехфазных приемников электрической энергии в качестве номинальных параметров указываются линейные напряжения и токи. Исходя из этого, целесообразней выражать мощность трехфазной цепи тоже через линейные напряжения и тока, поэтому подставим в формулу (6) линейные значения и получим:

Пример

К трехфазной электрической цепи с линейным напряжением U_л = U_ab = U_bc = U_ca = 380 В необходимо подключить трехфазный электроприемник, каждая фаза которого рассчитывается на фазное напряжение в 220 В и имеет активное сопротивление r_ф = 10 Ом и индуктивное сопротивление х_ф = 10 Ом, которые соединены последовательно. Необходимо определить мощности, углы сдвига между токами и напряжениями (cos φ) и фазные токи.

Решение

Каждая фаза потребителя электрической энергии рассчитана на напряжение в раз меньше номинального, то фазы потребителя нужно соединять в звезду. Поскольку нагрузка в данном случае симметричная, то нулевой провод (нейтраль) к потребителю можно не подводить.

Фазные тока, углы сдвига cos φ, а также полны сопротивления фаз будут иметь вид:

Активная, реактивная и полная мощности  приемника, а также любой фазы будут равны:

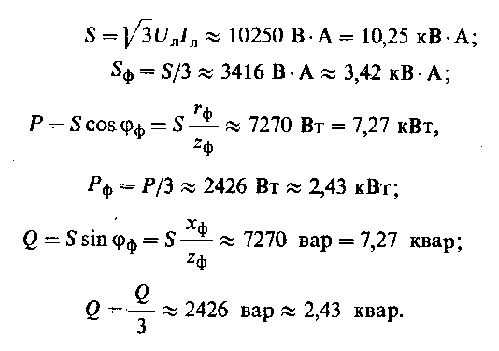
Векторная диаграмма для данной системы приводилась выше.

Несимметричная нагрузка при соединении приемников звездой

Нагрузка трехфазной электрической сети будет считаться несимметричной, если хотя бы одно из фазных сопротивлений не равно другим. Проще говоря, сопротивления фаз не равны, например: r_a = r_b = r_c, x_a = x_b ≠ x_c. В общем случае  считают, что несимметричная нагрузка возникает при отключении одной из фаз.

Возникает не симметрия чаще всего при подключении к трехфазной сети однофазных электроприемников. Они могут иметь различные мощности, режимы работы, различное территориальное расположение, что тоже влияет на величину фазной нагрузки.

В случае, когда необходимо подключить однофазные потребители электрической энергии, для более равномерной загрузки их делят на три примерно одинаковые по мощности группы.

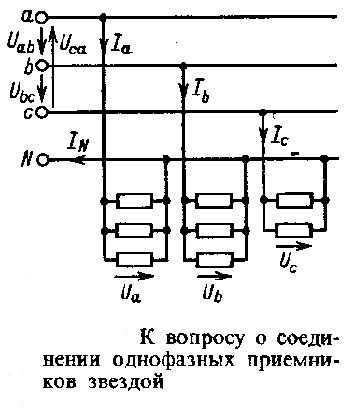
Один вывод однофазных потребителей подключают к одной из трех фаз, а второй вывод подключают к нейтральному проводу. Так как все электроприемники рассчитываются на одно напряжение, то в пределах каждой фазы они соединяются параллельно.

Главной особенностью электрической сети несимметричной нагрузкой является то, что она должна в обязательном порядке иметь нейтральный провод. Это объяснимо тем, что при его отсутствии величины фазных напряжений будут в значительной степени зависеть от величины не симметрии сети, то есть от величин и характера сопротивления каждой из фаз. Поскольку сопротивления фаз могут варьироваться довольно в широких пределах в зависимости от количества подключенных электроприемников, также широко будет варьироваться и напряжения на потребителях электрической энергии, а это недопустимо.

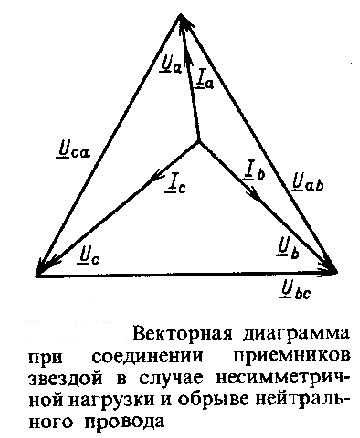
Для иллюстрации выше сказанного ниже приведена векторная диаграмма для трехфазной несимметричной цепи при наличии нейтрального провода:

Ниже приведена приведена векторная диаграмма для этой же цепи, но при отсутствии нулевого рабочего (нейтрального) провода:

Также можно посмотреть видео, где объясняется, что может произойти в электрической цепи при обрыве нулевого провода:

Необходимость нулевого провода станет еще более очевидной, если представить, что вам необходимо подключить однофазного потребителя к одной из фаз, при этом остальные две подключать нельзя, так как приемник рассчитан на фазное напряжение 220 В, а не на линейное 380В, как в таком случае получить замкнутый контур для протекания электрического тока? Только использовать нулевой рабочий проводник.

Для повышения надежности соединения электроприемников в цепь нулевого рабочего проводника не устанавливают коммутационную аппаратуру (автоматические выключатели

, предохранители или разъединители).

Фазные токи, углы сдвига, а также фазные мощности при несимметричной нагрузке будут различными. Для вычисления их фазных значений можно применить формулу (5), а вот для вычисления трехфазной мощности формула (6) уже не подходит. Для определения мощностей необходимо пользоваться выражением:

Если существует необходимость определения тока нейтрального провода, то необходимо решать задачу комплексным методом. Если существует векторная диаграмма, то определить ток можно по ней.

Пример

В осветительной электрической сети с напряжением в 220 В в фазе А включено 20 ламп, фазе В – 10 ламп, а в фазе С – 5 ламп. Параметры лампы U_ном = 127 В, Р_ном = 100 Вт. Необходимо определить ток нейтрального провода и каждой лампы.

Решение

Если учесть, что лампы накаливания имеют только активное сопротивление (реактивное слишком мало и им пренебрегают), то по формуле мощности определим ток лампы, а по закону Ома ее сопротивление:

Зная число и сопротивление ламп нетрудно определить сопротивления фаз, а также фазные токи:

Для определения тока в нейтральном проводе I_N решим задачу комплексным методом. Так как при сделанных ранее допущениях комплексные напряжения приемника равны комплексным ЭДС источника, получим:

Где комплексные значения фазных сопротивлений будут равны Z_a = 8,05 Ом, Z_b = 16,1 Ом, Z_с = 32,2 Ом.

Комплексные значения токов, а также действующее значение тока нейтрального провода будут иметь вид:

elenergi.ru

4.3. Трехфазные цепи при соединении приемников звездой

Соединение звездой при симметричной нагрузке. При соединении приемников звездой концы фаз приемника соединены в общий узел N’. При этом концы всех фаз генератора соединены в общий узел N, а начала фаз — с нагрузкой — звездой сопротивлений.

Если узлы N и N’ соединить проводом, называемым нейтральным, с сопротивлением Z_N, то получим четырехпроводную цепь (рис. 4.7, а). Сопротивления проводов, связывающих источник с нагрузкой, можно учесть в сопротивлениях нагрузки Z_a,Z_b,Z_c.

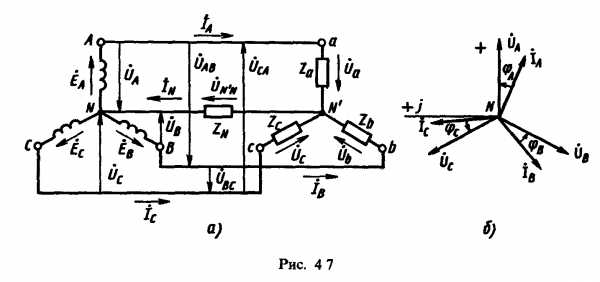
Так как при соединении звездой фазы генератора соединены последовательно с фазами нагрузки, линейные токи одновременно являются и фазными токами как в фазах генератора, так и в фазах нагрузки:

(4.8)

За условные положительные направления линейных токов I

А, I_В, I_С принимают направления от источника к нагрузке, а за положительное направление тока в нейтральном проводе – от нагрузки к источнику.

Согласно первому закону Кирхгофа, ток в нейтральном проводе

(4.9)

При симметричной нагрузке поэтому токи в фазах приемника равны по значению и сдвинуты по фазе на один и тот же угол относительно соответствующих напряжений, т. е. φ_A = φ_B = φ_C = φ. Векторная диаграмма напряжений и токов для симметрич­ной нагрузки представлена на рис. 4.7, б. Из диаграммы видно, что ток в нейтральном проводе равен нулю (I_N = 0), так как . Таким образом, если нагрузка равномерная, то необходимость в нейтраль­ном проводе отпадает. Трехфазная цепь без нейтрального провода яв­ляется трехпроводной.

Рассмотрим четырехпроводную цепь (рис. 4.7, а) более подробно. Найдем для этой цепи напряжение между нейтральными точками N и N’, или смещение нейтрали, по методу двух узлов:

(4.10)

где – комплексы проводимостей фаз приемника;Y_N= 1/Z_N -комплекс проводимости нейтрального провода. Так как при симметрич­ной нагрузке Ya = Yb = Yc, то (4.10) можно переписать в виде

(4.11)

При симметричной системе напряжений имеем

а значит, согласно (4.11), U_NN =0. Так как ток в нейтральном проводе то при симметричной нагрузкеI_N = 0. Следовательно, еще раз можно подчеркнуть, что при симметрич­ной нагрузке напряжение между нейтральными точками N и N’ и ток в нейтральном проводе равны нулю.

Согласно второму закону Кирхгофа, для контуров (см. рис. 4.7, а) NAaN’N, NBbN’N, NCcN’N находим

(4.12) Так как при симметричной нагрузке U_N’N =0, то из (4.12) следует, что

Итак, зная фазные напряжения и сопротивления нагрузки, находим токи в каждой фазе приемника:

(4-13)

Так как при симметричной нагрузке токи в фазах приемника равны, то достаточно определить ток только в одной из фаз трехфазной цепи.

Соединение звездой при несимметричной нагрузке. При несимметрич­ной нагрузке сопротивления приемника не одинаковы, т. е. Z_a ≠ Z_b ≠ Z_c. Для несимметричных нагрузок применяют четырехпроводные цепи, так как между точками N и N’ появляется напряжение U_N’N и напряжения на фазах нагрузки различны. При этом нарушается соотношение между фазными и линейными напряжениями причем на одних фазах нагрузки напряжение становится большим, а на других — меньшим, чем

Наличие нейтрального провода в цепи с несимметричной нагрузкой позволяет выравнивать напряжение на фазах приемника и поддержи­вать их неизменными, равными фазным напряжениям источника U_л /, т. е. нейтральный провод обеспечивает симметрию фазных напряжений приемника. Иначе говоря, при наличии нейтрального провода, когда Z_N = 0, даже при несимметричной нагрузке фазные напря­жения приемника равны друг другу и соблюдается соотношение между фазными и линейными напряжениями .

Если нагрузка несимметрична (Z_a ≠ Z_b ≠ Z_c) и нейтральный провод имеет конечное сопротивление Z_N, то напряжение U_N’N между нейтраль­ными точками N’ и N определяется по формуле (4.10), а напряжения на фазах нагрузки — по формулам (4.12). Тогда токи в схеме рис. 4.7, а

Если напряжения источника U_A, U_B, U_C образуют симметричную систему, то при отсутствии нейтрального провода и при U_N’N ≠ 0 напря­жения на фазе нагрузки U_a, U_b и U_c несимметричны, что видно из век­торной топографической диаграммы, приведенной на рис. 4.8. Особен­ностью этой диаграммы является то, что каждой точке электрической цепи А, В, С, N и N’ соответствует определенная точка на диаграмме.

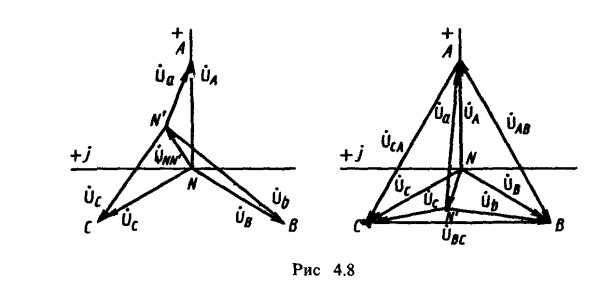
При этом расположение этих точек на диаграмме должно быть таким, чтобы отрезок, соединяющий любые точки на диаграмме, по длине и фазе определял напряжение между соответствующими точками цепи.

Напряжения на фазах нагрузки тем больше отличаются друг от друга, чем больше напряжение U_N‘N. Из выражения (4.10) и из топографи­ческой диаграммы (рис. 4.8) следует, что напряжение между нейтраль­ными точками U_N‘N будет изменяться при изменении нагрузки в любой фазе, при этом с изменением U_N‘N будет изменяться напряжение всех фаз приемника.

Чтобы напряжения на фазах нагрузки были одинаковыми, необхо­димо иметь U_N‘N= 0, что может быть получено двумя способами. Во-первых, выравниванием нагрузки в фазах приемника, когда Y_A = Y_B = Y_C = = Y_ф, а значит, согласно (4.10),

так как

Во-вторых, если имеется нейтральный провод с сопротивлением Z_N’N = 0 (или Y_N’N = ∞ ), то напряжение U_N‘N, согласно (4.10), также при­нимает нулевое значение независимо от нагрузки фаз. Для этого случая построена векторная диаграмма (рис. 4.9). При обрыве нейтрального провода (Z_N = ∞) и несимметричной на­грузке напряжение U_N‘N станет максималь­ным.

В фазах нагрузки могут возникнуть перенапряжения, поэтому в нейтральный провод плавкий предохранитель не ставят. Приемники электрической энергии мож­но подразделить на трехфазные и одно­фазные. К числу трехфазных относятся трехфазные электрические двигатели, имею­щие симметричные обмотки и обеспечиваю­щие равномерную нагрузку фаз. Такие электродвигатели включают в трехфаз­ную цепь звездой без нейтрального провода Однофазные приемники, к которым относятся электрические лампы, нагревательные приборы и ряд других приемников, всегда подключают к четырехпроводной цепи. Эти приемники подключаются на фазное напряжение, которое в раз меньше линейного напряжения сети.

Пример 4.1. К трехфазной линии напряжением Uл=380 В подключен несимметричный трехфазный приемник, соединенный звездой с нейтральным проводом (рис. а)). Активные и реактивные сопротивления фаз приемника соответственно равны: R_a = 19 Ом, X_a = 0 Ом, R_b= 8 Ом, Х_b = 6 Ом, R_с = 24 Ом, Х_c = 18 Ом. Сопротивлениями проводов можно пренебречь. Определить ток в фазах приемника, в линейных проводах и в нейтральном проводе.

а)

Рисунок к примеру 4.1.

Решение. Токи в линейных проводах и фазах приемника одинаковы и рассчитываются по закону Ома:

–

Фазное напряжение

Комплексные фазные напряжения:

Комплексные сопротивления фаз:

Токи в фазах приемника и проводах линии:

Ток в нейтральном проводе

Для построения топографической диаграммы напряжений выберем масштаб напряжений. В выбранном масштабе строим топографическую диаграмму напряжений. При построении векторной диаграммы токов учтем, что токи в фазах сдвинуты относительно фазных напряжений на разные углы сдвига фаз: φ_а =0 — нагрузка чисто активная (Х=0), φ_b = 36°52′ — нагрузка активно-индуктивная, φ_c = – 36⁰52’— нагрузка активно-емкостная.

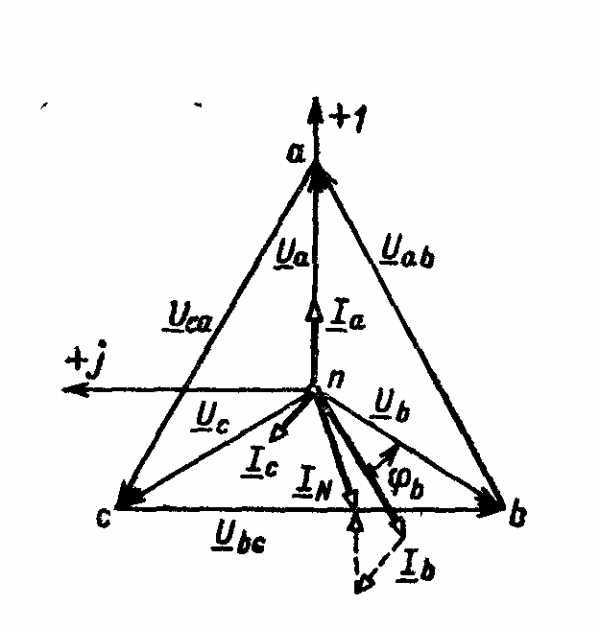Действующее значение тока в нейтральном проводе равно 16,14 А, а его начальная фаза ψ_N= 201⁰. На диаграмме (рис. б) строим векто­ры токов

б)

Рисунок к примеру 4.1.

с учетом углов сдвига фаз. Вектор тока в нейтральном прово­де можно построить двумя способами: или как сумму векторов или непосредственно отложить вектор I_N в соответствии с расчетными данными.

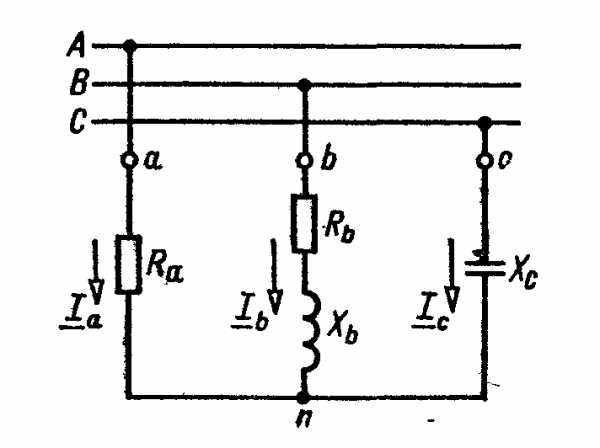Пример 4.2. К трехпроводной трехфазной сети с линейным напряже­нием Uл=220 В подключен приемник, фазы которого соединены звез­дой, (рис.а)). Заданы сопротивления R_а = 10 Ом, R_b = 5 Ом, Х_b = 9,66 Ом, Х_с = 10 Ом. Определить токи в ветвях, построить совмещенную топографическую диаграмму напряжений и векторную диаграмму токов.

а)

Рисунок к примеру 4.2.

Решение. Фазные напряжения источника образуют симметричную систему

Комплексные сопротивления фаз приемника:

их комплексные подводимости

Смещение нейтрали

б)

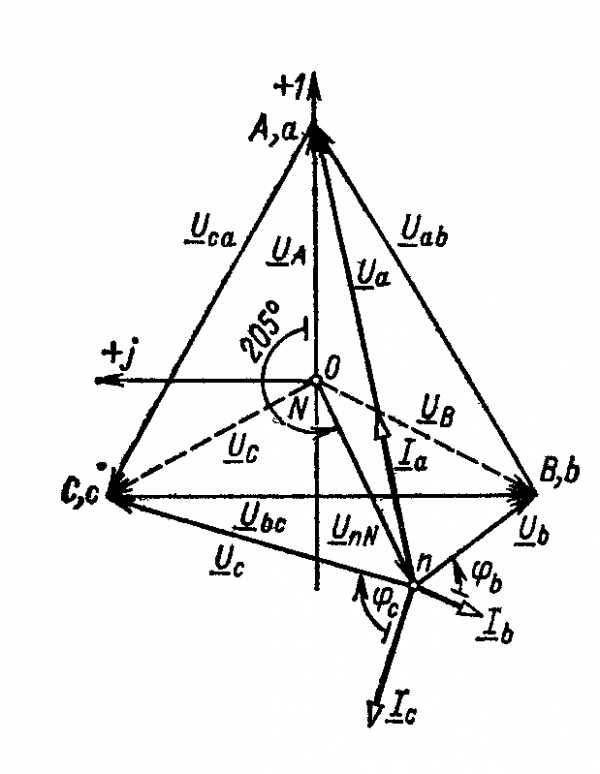
Рисунок к примеру 4.2.

Фазные напряжения приемника:

Фазные токи и токи в линии:

Для построения векторных диаграмм выбираем масштабы напря­жения и тока. Строим симметричную топографическую диаграмму на­пряжений генератора ( рис. б)) и вектор смещения нейтрали U_nN= 84e ^j205° В. Векторы, соединяющие точку n и точки а, b, с, соот­ветственно будут векторами фазных напряжений приемника U_a, U_b, U_c. Из точки n строим векторы токов I_a, I_b, I_с учетом сдвига фаз относи­тельно напряжений φ_a= 0°, φ_b= 60°, φ_c= — 90°.

Топографическая диаграмма напряжений показывает, что из-за смещения нейтрали симметрия фазных напряжений приемника наруша­ется: U_a= 206 В вместо U_ф = 127 В; U_c = 145,6 В; U_b=75,5 В.

studfiles.net

Как нарисовать радиально-симметричную пятиконечную звезду?

На самом деле, как вы заметили, в мире не существует равноправной симметричной пятисторонней звезды, которая бы удовлетворяла требованию иметь центр, где находится центр ограничительной рамки звезды. Системы изображения, как правило, обрезают излишки.

Центр объекта – сложная вещь. Центр ограничивающего прямоугольника редко приравнивается к центру объекта. К сожалению, центр – это размытое понятие, поэтому независимо от того, что вы выберете в качестве метрики центра, время от времени вы ошибаетесь. (подробнее об этом можно прочитать здесь .)

Теперь почти универсальные системы выбирают легкий путь и определяют ограничивающий прямоугольный центр как центр объекта. Это хорошо, если вы хотите, чтобы другой центр просто окружил ваш объект невидимым прямоугольником или кругом, который достаточно большой и центр, где вы хотите его. Он может касаться одного края, если вам нравится, но это не обязательно (и не обязательно самое компактное или беспроблемное представление).

Изображение 1 : вращаться вокруг центра bb.

В качестве альтернативы вы можете использовать группы, чтобы найти центр. По сути, сохраняет положение центра, так что теперь больше не имеет значения, какую форму имеет изображение. А вот живой SVG-пример использования метода группировки.

Что бы вам ни показалось проще, более поздний метод более компактен в сложных случаях или в тех случаях, когда вы считаете, что центр находится на краю изображения, поскольку вам нужно всего лишь сохранить 2 поплавка. Принимая во внимание, что если у вас есть растровое изображение с большим количеством пустого пространства, вы тратите больше памяти.

JollyJoker

+1 за создание «недорогого программного обеспечения» любого текстового редактора. Пример SVG – это как раз то, что нужно OP.

---

androidguy

Живой пример, похоже, радиально симметричен. Я не уверен, как вы пришли к точкам для его пути; Я, конечно, мог бы использовать защиту там, если бы мне не повезло со Sketch.

---

joojaa @androidguy Это радиально симметрично, см. codepen.io/anon/pen/zzPJoX?editors=1100 между точками угол 36 градусов. В любом случае используйте параметрическую функцию для круга.

---

Кайл Стрэнд

Вы, кажется, используете другое определение «ограничения», чем OP. Обратите внимание на это предложение из исходного вопроса: «Важно отметить, что самое большее (я думаю) 1 точка звезды коснется квадрата». Это указывает на то, что ограничивающий квадрат не является стандартным «ограничивающим прямоугольником», то есть прямоугольником минимального размера, содержащим звезду.

---

joojaa

@KyleStrand Но это не минимально, минимальная коробка имеет 3 точки в коробке, даже если они имеют общий центр. Форма растрового изображения может быть любой прямоугольной областью и не обязательно должна быть квадратной. Но да, минимальный прямоугольник в любой перпендикулярной ориентации касается 1 точки. Или, возможно, нет смысла касаться, если его повернуть. Я минимизирую функцию. Но не вменяемый движок рендеринга.

askentire.net

§60. Схема соединения «звездой»

Схема «звезда с нулевым проводом». При соединении фазных обмоток источника трехфазного тока (например, генератора) по схеме «звезда с нулевым проводом» концы его трех обмоток соединяют в общий узел 0, который называется нулевой точкой, или нейтралью источника (рис. 206). Приемники электрической энергии объединяют в три группы Z_A, Z_B и Z_c (фазы нагрузки), концы которых также соединяют в общий узел 0′ (нулевая точка, или нейтраль нагрузки). Обмотки источника соединяют с фазами нагрузки четырьмя проводами. Провода 1, 2 и 3, присоединенные к началам фазных обмоток (А, В, С), называют линейными. Провод 4, соединяющий нулевые точки 0 и 0′, называют нулевым, или нейтральным. Напряжения u_А, u_в и u_с между началами и концами обмоток отдельных фаз источника или фаз нагрузки Z_A, Z_B и Z_c называют фазными. Они равны также напряжениям между каждым из линейных проводов и нулевым проводом. При отсутствии потери напряжения в обмотках источника (при холостом ходе) фазные напряжения равны соответствующим э. д. с. в этих обмотках. Фазными токами i_A, i_B, i_c называют токи, протекающие по обмоткам источника или фазам нагрузки Z_A, Z_B и Z_c. Напряжения u_AB, u_BC, u_CA между линейными проводами и токи, проходящие по этим проводам, называют линейными.

Примем условно за положительное направление токов i_A, i_B и i_c в фазах источника — от конца соответствующей фазы к ее началу,

Рис. 206. Схема «звезда с нулевым проводом», направление в ней линейных и фазных токов и напряжений

Рис. 207. Векторные диаграммы напряжений для схемы «звезда с нулевым проводом»

в фазах нагрузки — от начала к концу, а в линейных проводах — от источника к приемнику. Будем считать положительными напряжения u_А, u_B и u_C в фазах источника и нагрузки, если они направлены от начала фаз к концам, а линейные напряжения u_АВ, u_BC, u_СА — если они направлены от предыдущей фазы к последующей.

Из рис. 206 следует, что в схеме «звезда» линейные токи равны фазным, т. е. I_л = I_ф, так как при переходе от фазы источника или нагрузки к линейному проводу нет каких-либо ответвлений. Мгновенные значения напряжений согласно второму закону Кирхгофа:

u_АВ = u_А – u_B; u_BC = u_B – u_С; u_СА = u_С – u_А.

Переходя от мгновенных значений напряжений к их векторам, имеем:

?_АВ = ?_А – ?_B; ?_BC = ?_B – ?_С; ?_СА = ?_С – ?_А.

Следовательно, линейное напряжение равно разности векторов соответствующих фазных напряжений. По полученным векторным уравнениям можно построить векторную диаграмму (рис. 207, а), которую можно преобразовать в диаграмму (рис. 207,б). Из этой диаграммы видно, что в симметричной трехфазной системе векторы линейных напряжений ?_AB, ?_ВС, ?_СА образуют равносторонний треугольник ABC, внутри которого расположена симметричная трехлучевая звезда фазных напряжений ?_А, ?_В, ?_С. В равнобедренных треугольниках АОВ, ВОС и СОА основание равно U_л две другие стороны — U_ф и острый угол между этими сторонами и основанием составляет 30°. Следовательно,

U_л = 2U_ф cos 30° = 2U ?3 / 2 = ?3 U_ф

Таким образом, в трехфазной системе, соединенной по схеме «звезда с нулевым проводом», линейное напряжение больше фазного в ?З раз. Величина ?З = 1,73 положена в основу шкалы номинальных напряжений переменного тока: 127, 220, 380 и 660 В. В этом ряду каждое следующее значение напряжения больше предыдущего в 1,73 раза.

В нулевом проводе проходит ток i0, мгновенное значение которого равно алгебраической сумме мгновенных значений токов, проходящих в отдельных фазах: i0 = iA+iB+ic.

Переходя от мгновенных значений токов к их векторам, имеем:
?₀=?_A+?_B+?_C.

Векторы токов ?_А, ?_В и ?_С сдвинуты относительно векторов соответствующих напряжений ?_A, ?_B, ?_С на углы ?_A, ?_B, ?_C (рис. 208, а). Значения этих углов зависят от соотношения между активным и реактивным сопротивлениями, включенными в данную фазу. На этой же диаграмме показано сложение векторов ?_А, ?_В и ?_C для определения вектора тока ?₀. Обычно ток ?₀ меньше токов

Рис. 208. Векторные диаграммы напряжений и токов в отдельных фазах для схемы «звезда с нулевым проводом» при неравномерной (а) и равномерной (б) нагрузках фаз

I_A, 1_В и I_C в линейных проводах, поэтому нулевой провод имеет площадь поперечного сечения, равную или даже несколько меньшую площади сечения линейных проводов.

В схеме «звезда с нулевым проводом» приемники электрической энергии можно включать на два напряжения: линейное U_л (при подключении к двум линейным проводам) и фазное U_Ф (при подключении к нулевому и одному из линейных проводов).

Схема «звезда без нулевого провода». При равномерной или симметричной нагрузке всех трех фаз, когда во всех фазах включены одинаковые активные и реактивные сопротивления (R_A =R_B = R_C и Х_A=Х_В=Х_С), фазные токи i_A, i_B и i_C будут равны по величине и сдвинуты от соответствующих фазных напряжений на равные углы. В этом случае получаем симметричную систему токов, при которой токи i_A, i_B, i_C будут сдвинуты по фазе друг относительно друга на угол 120°, а ток i₀ в нулевом проводе в любой момент времени равен нулю (рис. 208,б).

Очевидно, что при равномерной нагрузке можно удалить нулевой провод и передавать электрическую энергию источника к приемнику по трем линейным проводам 1, 2 и 3 (рис. 209). Такая схема называется «звезда без нулевого провода». При трехпровод-ной системе передачи электрической энергии в каждое мгновение ток по одному (или двум) проводу проходит от источника трехфазного тока к приемнику, а по двум другим (или одному) протекает обратно от приемника к источнику (рис. 210). Векторная диаграмма напряжений для схемы «звезда без нулевого провода» при равномерной нагрузке фаз будет такая же, как и для схемы «звезда с нулевым проводом» (см. рис. 207). Такими же будут и соотношения между фазными и линейными токами и напряжениями:

I_л = I_Ф и U_л = ?3 U_Ф

Следует отметить, что схема «звезда без нулевого провода» может быть применена только при равномерной нагрузке фаз. Практически это имеет место лишь при подключении к источникам трехфазного тока электрических двигателей, так как каждый трехфазный электродвигатель снабжен тремя одинаковыми обмотками, которые равномерно нагружают все три фазы. При неравномерной нагрузке напряжения на отдельных фазах нагрузки будут различными. На некоторых фазах (с меньшим сопротивлением) напряжение уменьшится, а на других увеличится по сравнению с нормальным, что является недопустимым.

Рис. 209. Схема «звезда без нулевого провода»

Практически неравномерная нагрузка фаз возникает при питании трехфазным током электрических ламп, так как в этом случае распределение тока между всеми тремя фазами не может быть гарантировано (отдельные лампы могут включаться и выключаться в индивидуальном порядке). Особенно опасны в схеме «звезда без нулевого провода» обрыв или короткое замыкание в одной из фаз. Можно показать путем построения соответствующих векторных диаграмм, что при обрыве в одной из фаз напряжение в других двух фазах уменьшается до половины линейного, вследствие чего лампы, включенные в эти фазы, будут гореть с недокалом. При коротком замыкании в одной из фаз напряжение в других фазах увеличивается до линейного, т. е. в ?З раз, и все лампы, включенные в этих фазах, перегорят. Поэтому при схеме «звезда с нулевым проводом» во избежание разрыва цепи нулевого провода в ней не устанавливают предохранители и выключатели.

Рис 210. Кривые изменения токов в линейных проводах (а) при трехпроводной системе и направление в них токов в различные моменты времени (б в, г)

electrono.ru

Треугольная галактика продемонстрировала невероятно симметричное расположение звезд

Пришло время сменить картинки на рабочем столе компьютеров. Ведь Хаббл вновь удивил своими возможностями. Как только удается телескопу находить такие кадры — вопрос еще тот. Но новые фотографии продемонстрировали ученым, что звезды в галактиках могут быть на удивление симметричными. Во всяком случае, такое расположение замечено в Треугольной галактике.

Эта галактика — одна из ближайших к Земле. И Хабблу удалось запечатлеть звездную спираль этой системы аж в пятидесяти четырех вариантах. Благодаря такому охвату удалось получить изображение галактики, которую научно называют M33. В ней живет и развивается порядка двадцати пяти миллионов звезд. Это те, что называют видимыми.

Галактика Треугольник располагается в так называемой Местной группе. Здесь находится несколько галактик. Вот только самыми знаменитыми считаются галактики: Треугольник, Андромеда и наш родной Млечный путь.

Сегодня о Треугольнике ученые знают не так уж и много. Пока известно, что звездообразование здесь идет крайне интенсивно. Примерно в десять раз активней, чем в Андромеде.

Вообще, Треугольник — это своего рода звездный интроверт. Он не любит активно взаимодействовать с другими галактиками. Разве что вынужденно. Поэтому-то и историю этой системы пока не удалось изучить. Поэтому исследователи очень надеются на то, что им все же удастся узнать гораздо больше о соседе и благодаря этому положить еще немного крупинок в копилку знаний о том, как образуются звезды, как живут разные галактики и каким путем идет в них эволюция.

Поделиться

Твитнуть

Поделиться

Плюсануть

Поделиться

Твитнуть

Поделиться

Плюсануть

mks-onlain.ru

Как выглядели бы звезды, если бы их лица были абсолютно симметричными.

Люди с пропорциональными чертами лица всегда кажутся более привлекательными. Разумеется, абсолютно симметричных лиц не бывает, даже у признанных красавцев и красоток.

Мы решили пофантазировать, как бы выглядели знаменитости с идеально симметричной внешностью. Каждое фото слева показывает зеркальное  отражение левой стороны лица. Фото справа — отражение правой стороны лица.

Результат нас просто шокировал. Смотри сам!

1. Марион Котийяр

2. Брэд Питт

3. Райан Гослинг

4. Ванесса Паради

5. Дензел Вашингтон

6. Джон Чо

7. Натали Портман

8. Бейонсе

9. Леа Сейду

10. Джон Хэмм

11. Рианна

12. Адель

13. Канье Уэст

14. Ким Кардашьян

15. София Вергара

Как видишь, симметричное лицо — это не только неестественно, но даже жутко. Неудивительно, что звезды никогда не прибегают к этой опции, если обрабатывают свои фото в Фотошопе.

А чье лицо потрясло тебя больше всего? Пиши в комментариях и поделись статьей с друзьями.

ofigenno.com

38. Расчет симметричных трехфазных цепей в соединении «звезда».

Многофазный приемник и вообще многофазная цепь называются симметричными, если в них комплексные сопротивления соответствующих фаз одинаковы, т.е. если . В противном случае они являютсянесимметричными. Равенство модулей указанных сопротивлений не является достаточным условием симметрии цепи. Так, например трехфазный приемник на рис. 1,а является симметричным, а на рис. 1,б – нет даже при условии: .

Если к симметричной трехфазной цепи приложена симметричная трехфазная система напряжений генератора, то в ней будет иметь место симметричная система токов. Такой режим работы трехфазной цепи называетсясимметричным. В этом режиме токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг по отношению к другу на угол . Вследствие указанного расчет таких цепей проводится для одной –базовой – фазы, в качестве которой обычно принимают фазу А. При этом соответствующие величины в других фазах получают формальным добавлением к аргументу переменной фазы  А  фазового сдвига при сохранении неизменным ее модуля.Так для симметричного режима работы цепи на рис. 2,а при известных линейном напряжении и сопротивлениях фазможно записать,гдеопределяется характером нагрузки.Тогда на основании вышесказанного;.

Комплексы линейных токов можно найти с использованием векторной диаграммы на рис. 2,б, из которой вытекает:

При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется с помощью двух основных приемов:Все треугольники заменяются эквивалентными звездами. Поскольку треугольники симметричны, то в соответствии с формулами преобразования «треугольник-звезда»  . Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам которого определяются соответствующие величины в других фазах.

45. Опытное определение параметров схемы замещения трансформатора.

R1 R2 – активное сопротивления первичной и вторичной обмоток.

X1 X2 – отражает магнитные потоки первичной и вторичной обмотки.

X0 – отражает действия основного магнитного потока.

I1 I2 – токи первично и вторичной обмотки.

Опыт холостого хода. Опытное определение параметров схемы замещения трансформатора производится по данным опыта холостого хода и короткого замыкания.

Схема опытов холостого хода однофазного (т = 1) и трехфазного (т = 3) двухобмоточных трансформаторов приведены на рис. 14-10. Первичная обмотка трансформатора подключается на синусоидальное напряжение, а вторичная обмотка разомкнута. Измеряются первичные напряжения U_o = U_w, ток /₀ = 1_г и мощность Р_о = Pi, а также вторичное напряжение U_w.Из данных опыта для однофазного трансформатора определяются полное, активное и индуктивное сопротивления холостого хода:

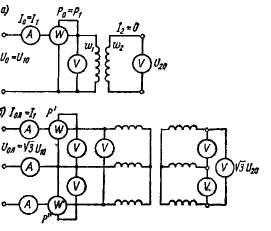
Рис. 14-10. Схемы опытов холостого хода однофазного (а) и трехфазного (б)двухобмоточных трансформаторов.

Для трехфазного трансформатора по показаниям трех амперметров и вольтметров определяются средние значения линейного тока /_Ол и линейного напряжения 1/_Ол, а по показаниям ваттметров — мощность холостого хода трех фаз Р_о = Р’ + Р”> Физический смысл имеют только значения сопротивлений, рассчитанные для фазы обмотки. Поэтому необходимо принять во внимание схему соединения обмотки. В случае соединения первичной обмотки в звезду. Коэффициент трансформации трехфазного трансформатора может рассчитываться по фазным напряжениям (&) или по линейным напряжениям (&_л). Для теории трансформатора имеет значение первое из указанных значений коэффициента трансформации.

Так как г_х <^ г_м, то потери холостого хода практически представляют собой потери в стали сердечника, включая потери от вихревых токов в стенках бака в режиме холостого хода.Опыт холостого хода производят обычно для ряда значений U_o: от U_o а* 0,3 U_n до U_o « 1,1 U_o насыщение сердечника увеличивается, вследствие чего /₀ растет быстрее U_Q. Поэтому z₀ и х₀ с ростом U_o уменьшаются. Так как Р_п г^ Е² ^ U², а Р_о растет быстрее Щ, то г₀ с ростом Uо также . уменьшается. По характеристикам холостого хода устанавливаются значения соответствующих величин для U_o == U_H.

Опыт короткого замыкания производится по схемам рис. 14-13. Вторичные обмотки замыкаются накоротко, а к первичным обмоткам во избежание перегрева и повреждения трансформатора подводится пониженное напряжение с таким расчетом, чтобы ток находился в пределах номинального.

Полное z_K, активное г_к и реактивное х_к сопротивления короткого замыкания рассчитываются по формулам, аналогичным для случая холостого хода.

studfiles.net