Ментальная Арифметика на Пальцах
Вы когда-нибудь задумывались, почему у восточных сорабанских счетчиков- математиков, которые занимаются Ментальной Арифметикой есть 4 отдельных бусинки? Они находится в базе 10, а не 4 или 5, так зачем организовать такой счет таким образом?
Ответ счета в Ментальной Арифметики может исходить только с объяснением математики пальцев. Если вы посмотрите на этот аккуратный способ подсчета до 99 на ваших двух руках, то вы поймете Соробан – Абакус! Четыре бусинки означают четыре пальца на руке и отдельную бусину для большого пальца это нашу пятерку.
Человеческая рука несет пять пальцев; у двух рук их десять. Несомненно, этот факт отвечает за универсальное принятие десятичной системы.
Дети учатся рассчитывать, считая пальцы в математике, сначала до 5 с одной стороны, а затем до 10 на две руки. Тем не менее, есть простой способ подсчитать до 10 с помощью всего 5 пальцев одной руки и до 100, используя обе руки.
Вот как это сделать:
Сложенный кулак может стоять на 10, если вы не планируете использовать секундную стрелку или 0, если вы это сделаете:
Вторая рука используется таким же образом, но для подсчета в математике 10 секунд:
С фотографиями и скриншотами из онлайн-счетов Soroban мы можем показать эту идею. Он работает лучше всего, если вы считаете. Сначала используйте четыре пальца правой руки для подсчета 1, 2, 3, 4. Это соответствует четырем шарикам в первом ряду Соробана, показанным желтым.
Затем вещи становятся немного более абстрактными. Большой палец — 5, сам по себе, точно так же, как и одинокий желтый шарик. Мы переходим от прямого подсчета к символам или иначе образности:
Вы добавляете пальцы в большой палец, чтобы подсчитать 6, 7, 8, 9. Представьте, что маленький ребенок играет с традиционными играми с пальцами с родителями. Дети могут мгновенно распознавать (сублицировать) количества от 1 до 4, но подсчет западных пальцев проходит до 10 — намного выше диапазона субтитизации. В отличие от подсчета западных пальцев, эта система вводит группы и символы (большой палец — 5), а также добавление, как только вы покидаете диапазон субтитизации. Другими словами, система следит за тем, как работают умы детей.
Что происходит, когда вы достигаете 10? Что-то очень полезное и захватывающее! Вы можете использовать другую руку, которая означает значение нового места — и новый ряд бус на абакусе. Цифры, бусины и пальцы — все вместе, как рука в перчатке.
Это интересно, читайте также:
Ментальная арифметика обучение для педагогов
Ментальная Арифметика методика
Поурочное планирование в Ментальной Арифметике
Как считать на абакусе
Вот еще одно отличие этой системы от подсчета ваших 10 пальцев. Вы можете сосчитать весь путь до 99 на ваших двух руках!
И если вы объедините силы с другом, вы можете показать еще большие цифры.
Вот видео, показывающее, как считать весь путь от 1 до 99:
Ментальная Арифметика удивительная наука, которая помогает понимать самую из всех точных наук нашу любимую математику. Изучайте и любите математику, она откроет вам много тайн, которые всегда очевидны и интересны. Ваша Ментальная Арифметика.
Сколько цифр числа Пи вы помните? Можете умножить 97 на 96 в уме? Мы подобрали несколько мнемонических приемов и математических трюков.
Операции с дробями
Сложить две дроби, у которых в числителе стоит единица, очень просто: нужно найти сумму знаменателей и поделить на их произведение:
Для более сложных случаев существует метод бабочки. Попробуем с его помощью сложить ¾ и ⅖.
- Для начала перемножаем по диагонали числители и знаменатели двух дробей.
- Затем складываем полученные произведения – это будет числитель искомого результата.
- Перемножаем знаменатели исходных дробей между собой и получаем знаменатель результата.
- Осталось только сократить полученную дробь, если это возможно.
Вычитание осуществляется точно так же, только на втором шаге нужно найти не сумму, а разность двух значений.
Пара математических трюков для умножения на 9
Запомнить таблицу умножения на 9 очень просто: она симметричная.
А для быстрых вычислений можно использовать собственные руки.
- Пронумеруем пальцы от 1 до 10.
- Найдем палец, соответствующий множителю девятки.
- Теперь посчитаем пальцы слева от выбранного и узнаем первую цифру ответа.
- Чтобы найти вторую, нужно посчитать пальцы справа.
Для примера, умножим 4 на 9:
А теперь посложнее:
В буквальном смысле посчитали на пальцах.
Умножение на 11
Еще одно удобное число – 11. При умножении на него первая и последняя цифры результата заранее известны, а остальные получаются путем попарного сложения разрядов исходного числа.
Для примера умножим 11 на 32:
- Первая цифра результата равна первой цифре множителя – это 3.
- Последняя цифра результата соответствует последней цифре множителя – это 2.
- Найти оставшуюся цифру можно, сложив первую и последнюю (3 + 2 = 5).
Слишком просто? Давайте возьмем пример посложнее и умножим 11 на 76:
Сумма цифр (7+6) здесь состоит из двух разрядов (13), а не из одного, как в предыдущем примере. Поэтому значение первого разряда (1) пришлось прибавить к первой цифре результата (7).
А теперь настоящий вызов: умножим 11 на 25816! Если вы сможете сделать это в уме, вы великолепны! Если нет, то воспользуйтесь этим методом.
Начинаем как раньше, с определения первой и последней цифр. А затем заполняем пропуски, складывая цифры попарно, начиная с конца:
- 6 + 1 = 7 – второй разряд;
- 1 + 8 = 9 – третий разряд;
- 8 + 5 = 13 – тройка занимает четвертый разряд, а единица – пятый;
- 5 + 2 = 7 – тоже идет в пятый разряд и объединяется с единицей.
Неплохо, правда?
Умножение больших чисел
Отличный метод для умножения чисел, близких к 100. С малыми значениями работать гораздо проще, чем с большими, поэтому мы заменим сами множители на их разность с сотней.
Вычитая из 100 числа 96 и 97 получим 4 и 3 – теперь это наши основные операнды.
Чтобы получить начало результата, сложим 3 и 4 и вычтем результат из 100 (100 – 7 = 93).
Последние два разряда – это произведение операндов (3 х 4 = 12). Обратите внимание, если получилось число меньше 10, перед ним следует написать 0, чтобы занять оба разряда.
Теперь в ваших руках довольно эффектное умение, можете удивлять друзей.
Число Пи
Запомнить первые 7 цифр числа Пи поможет английский мнемоник
How I wish I could calculate Pi
Количество букв в каждом слове равно соответствующей цифре.
Математические пирамиды
Два замечательных примера арифметической симметрии, которые вы можете использовать для быстрых вычислений или математических трюков.
Пирамида единиц:
И умножение на 8:
От Цельсия до Фаренгейта и обратно
Приходилось когда-нибудь переводить температуру по Цельсию в градусы Фаренгейта? Формула несложная, но запоминается плохо:
градусы Цельсия * 1.8 + 32 = градусы Фаренгейта
Для приблизительных подсчетов можно использовать более удобные значения: умножать на 2 и прибавлять 30.
Обратное преобразование состоит в вычитании 32 и делении на 1.8. Здесь также можно использовать упрощенную формулу:
А сколько математических трюков знаете вы?
Хватит фокусов, теперь о серьезной математике:
любой может освоить двоичную систему
Все думают, что на пальцах одной руки можно показать только 5 чисел. На самом деле -— любое число от 1 до 31!А если взять пальцы обеих рук — то от 1 до 1023!
Не верите?
Попробуйте сами!
Для этого вам понадобится…
А вот такие символы для чисел использовали в XVI веке
Сначала — подписать свои пальцы, начиная с мизинца.
Пусть мизинец означает 1,
средний палец — 4,
указательный палец — 8,
а большой — 16.
Тогда мы легко можем “собрать” любое число от 1 до 31 в виде суммы из нескольких слагаемых.
Например, 6 = 2+ 4,
а 13 = 8 + 4 + 1.
(Это называется двоичная система, и ею пользуются все компьютеры!)
И если мы палец поднимаем, то мы это слагаемое “берём”, а если палец прячем, то не берём.
Тогда это — число 1 + 4 + 16 = 21
А теперь посмотрим на такую закономерность.
Это число 3, то есть 1 + 2.
Мы использовали соседние пальцы, мизинец и безымянный.
Теперь попробуем сделать число в 2 раза больше, то есть 6.
Мы снова поднимаем соседние пальцы, на этот раз безымянный и средний.
И неудивительно,
6= 2 + 4.
Попробуем показать на пальцах число ещё в 2 раза больше!
Снова соседние пальцы, на этот раз средний и указательный.
12 = 4 + 8.
Теперь вы легко угадаете следующее число:
Это число …
А это число 5, показанное на пальцах.
5 = 1 + 4.
Попробуем сдвинуть на 1 палец правее и проверим нашу идею.
Получилось!
10 = 2 + 8.
И это не так уж удивительно, ведь сдвигая на 1 палец вбок мы увеличиваем каждое слагаемое ровно в 2 раза!
Вместо 1 берём 2, а вместо 4 — берём 8!
Теперь вы сами можете показать на пальцах 20, для этого вам понадобится показать
.Возьмём, к примеру, такое число:
Это
Если мы не используем в записи числа мизинец, то это число можно разделить пополам,
“сдвинув” влево все пальцы, то есть показав вместо безымянного — мизинец, вместо указательного — средний, а вместо среднего — большой палец.
Мы получим:
1 + 4 + 8 = 13, то есть ровно половину от предыдущего числа!
А теперь отгадайте это число:
.
И скажите, можем ли мы на пальцах показать половину этого числа?
А если мы захотим продолжить счёт на пальцах, то какое число надо написать на следующем пальце?
.Для того, чтобы узнать это, достаточно сложить все числа, и добавить 1,
или же… увеличить в 2 раза самое большое из наших, написанных на пальцах, кодов.
У нас самое большое число было 16,
а сумма всех 5 пальцев была 1 + 2 + 4 + 8 + 16 = 31.
Если мы добавим 1, то… как раз получим 16 + 16.
Как это получается?
Смотрите на картинку!
Если мы решим использовать все 10 пальцев, то мы сможем показать число 1023!!
любой может освоить двоичную систему
Все думают, что на пальцах одной руки можно показать только 5 чисел. На самом деле -— любое число от 1 до 31!А если взять пальцы обеих рук — то от 1 до 1023!
Не верите?
Попробуйте сами!
Для этого вам понадобится…
А вот такие символы для чисел использовали в XVI веке
Сначала — подписать свои пальцы, начиная с мизинца.
Пусть мизинец означает 1,
безымянный палец — 2,
средний палец — 4,
указательный палец — 8,
а большой — 16.
Тогда мы легко можем “собрать” любое число от 1 до 31 в виде суммы из нескольких слагаемых.
Например, 6 = 2+ 4,
а 13 = 8 + 4 + 1.
(Это называется двоичная система, и ею пользуются все компьютеры!)
И если мы палец поднимаем, то мы это слагаемое “берём”, а если палец прячем, то не берём.
Тогда это — число 1 + 4 + 16 = 21
А теперь посмотрим на такую закономерность.
Это число 3, то есть 1 + 2.
Мы использовали соседние пальцы, мизинец и безымянный.
Теперь попробуем сделать число в 2 раза больше, то есть 6.
Мы снова поднимаем соседние пальцы, на этот раз безымянный и средний.
И неудивительно,
6= 2 + 4.
Попробуем показать на пальцах число ещё в 2 раза больше!
Снова соседние пальцы, на этот раз средний и указательный.
12 = 4 + 8.
Теперь вы легко угадаете следующее число:
Это число …
А это число 5, показанное на пальцах.
5 = 1 + 4.
Попробуем сдвинуть на 1 палец правее и проверим нашу идею.
Получилось!
10 = 2 + 8.
И это не так уж удивительно, ведь сдвигая на 1 палец вбок мы увеличиваем каждое слагаемое ровно в 2 раза!
Теперь вы сами можете показать на пальцах 20, для этого вам понадобится показать
.Возьмём, к примеру, такое число:
Это
Если мы не используем в записи числа мизинец, то это число можно разделить пополам,
“сдвинув” влево все пальцы, то есть показав вместо безымянного — мизинец, вместо указательного — средний, а вместо среднего — большой палец.
Мы получим:
1 + 4 + 8 = 13, то есть ровно половину от предыдущего числа!
А теперь отгадайте это число:
.
И скажите, можем ли мы на пальцах показать половину этого числа?
А если мы захотим продолжить счёт на пальцах, то какое число надо написать на следующем пальце?
.Для того, чтобы узнать это, достаточно сложить все числа, и добавить 1,
или же… увеличить в 2 раза самое большое из наших, написанных на пальцах, кодов.
У нас самое большое число было 16,
Если мы добавим 1, то… как раз получим 16 + 16.
Как это получается?
Смотрите на картинку!
Если мы решим использовать все 10 пальцев, то мы сможем показать число 1023!!
Цифры, на пальцах.: genntal — LiveJournal
Казалось бы, что ещё нового можно сказать об арабских цифрах?После того, как наши первобытные фигуры цифр наглядно обрисовались здесь в плетёных узелках из упругих полосок, мне стало интересно, по какому принципу они округлились? Посмотрев материал о символах римских цифр, составленных из пальцев рук, попыталась строить фигуры из пальцев и посмотреть, как это будут выглядеть. В боковой плоскости римские цифры I, II, III, IV, сливаются в похожие фигуры и почти неразличимы, как и оставшиеся две – L, V. В эксперименте с другим набором и формой пальцев, крутя, вертя и разглядывая контуры под разными углами, почти сразу обнаружилось удивительное сходство новых силуэтов с современными цифрами.
Небольшая игра теней и… убедитесь сами:
Глаза и логика меня не обманывают? Новые контуры фигур из пальцев это вполне современные цифры?
Логика простая – в жизни бывают случаи, когда безопаснее молчать, чем говорить и тогда в ход идут жесты.
Указательным пальцем мы показываем на важный для случая предмет и этим же пальцем подзывам к себе человека. Если рот занят по какой-то причине, или не слышно из-за шума, то тоже показываем руками и на пальцах.
Вот как так могло получиться, что мои цифровые жесты больше похожи на арабские чем сами арабские?
А ведь я складывала пальцы не случайным образом, а в строгой арифметической последовательности:
1 – указательный;
2 – большой и указательный;
3 – большой, указательный и средний;
4 – большой, указательный, средний и безымянный (мизинец лежит горизонтально).
5 – кулак, но не сжат плотно;
6 – средний палец;
7 – указательный горизонтально и средний;
8 – указательный+ большой+средний;
9 – все вместе, кроме мизинца;
0 – все вместе(ноготь к ногтю).
Подушечки пальцев – как это может быть, что в шрифтах используются утолщения на концах линий похожие на эти самые подушечки?
В полном образе цыфры утверждаешься ещё и самой формой движения. Это важные движения, но их пока оставлю за кадром. Скажу только, что некоторые из этих движений удивительным образом совпадают по названию с названиями наших цифр.
Обратите внимание – мы показываем большой палец в знак высшей похвалы. Высший балл, пятёрка в оценках. Обе фигуры на рисунке под номерами 5/1 и 5/2 – суть одно и то же.
Проверте, может я что-то притянула за уши или подстроила, как в театре теней и у вас получатся другие комбинации.
В детстве мне было непонятно, почему старики так странно выписывают цифры? Нет не торопливо и случайно, а тщательно и старательно копируя казавшиеся мне некрасивыми, непропорциональными, несимметричными, незакономерно логичными и несовременными, графические особенности?
Примерно так (чуть крикатурно получилось):
Этот странный курносый носик у однёрки; хилая, пустая двойка; плоскоголовая, вжавшая шею, с опущенным козырьком тройка; зазнаесто-горделивая, брюхатая, в низком приседе четвёрка; насупившаяся бука пятёрка; клюющая носом, пузатая шестёрка; горбатая, приземистая семёрка с кинжалом наперевес; кособокая восьмёрка с маленькой головкой, сплющенная и завалившаяся на бок; как бы поскользнувшаяся девятка и огурцеобразный ноль – все эти на вид странности казались символом патриархальной уходящей эпохи. Именно патриархальной, потому, что такие особенности письма замечала только у пожилых мужчин. Может быть это совпадение и графика тех людей дань старым образцам шрифтов и особенностей подчерка? А, возможно, просто срабатывала зрительная память на особенности цифровых фигур из пальцев, которые отличаются своей разнообразной асимметрией от симметричных фигур из узлов, которые ближе женскому рукоделию.
Непонятно, как так получилось, что очевидные и простые фигуры цифр европейцы не замечали? Странно ещё и потому, что Хэллоуин это развлечение, основанное на игре света и тени. Глаз людей остро воспринимал и хорошо ассоциировал любые силуэты теней. Это был один из элементов, обеспечивающих выживание. Ещё в средине прошлого века художники зарабатывали тем, что вырезали ножницами на глаз профили и фигурки из чёрной и белой бумаги.
Счёт на пальцах: viata — LiveJournal
Римский легионер входит в бар, показывает бармену два пальца и говорит: “Пять бутылок для меня и моих друзей!”Самое забавное в этой шутке, что отчасти она верна: разные народы действительно считают на пальцах по-разному, и древние римляне действительно показывали числа на пальцах иначе, чем мы. Примерно вот так: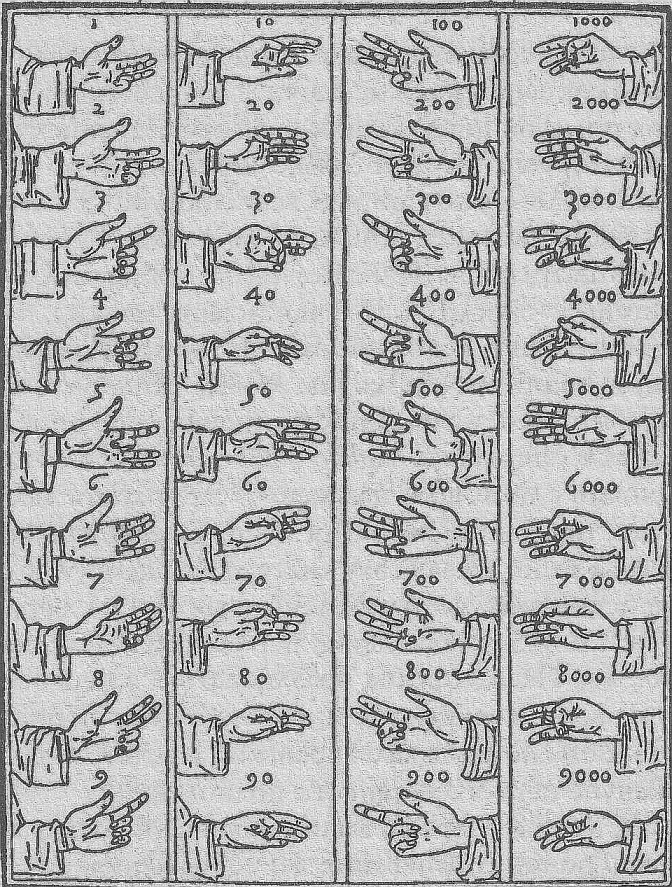
Эта система активно использовалась по всей Европе и Средиземноморью в начале нашей эры и довольно часто упоминается в текстах того времени, а также используется в изобразительном искусстве, когда персонажи картин или статуи показывают те или иные символичные числа.
На основе этой римской системы в средневековой Европе возникла другая, описанная Бедой Достопочтенным:
В арабском мире в ту же эпоху тоже знали европейский пальцевый счёт, но использовали и свой собственный, позволявший договариваться о цене не глядя и незаметно для окружающих, накрыв руку продавца и покупателя. Вот описание этой системы из Википедии:
“Прикосновение к вытянутому указательному пальцу продавца, в зависимости от цены и используемых денежных единиц, будет означать 1, 10 или 100. Одновременное прикосновение к двум, трём или чётырём пальцам продавца будет означать соответственно 2 (20, 200), 3 (30, 300) или 4 (40, 400). Касание открытой ладонью указывает на число 5, 50 или 500. Дотронуться до мизинца означает 6, 60 или 600, безымянный палец — 7, 70 или 700, средний палец — 8, 80 или 800, согнуть указательный палец — 9, 90 или 900, коснуться Большого пальца — 10, 100 или 1000. При этом счислении может соблюдаться последовательность числовых степеней, например число 78 задаётся касанием безымянного пальца продавца, а затем — его среднего пальца. Постукивание по указательному пальцу продавца в направлении от среднего сустава к кончику пальца — предложение о снижении цены вдвое (1/2), на четверть (1/4) или на восьмую часть (1/8) от первоначальной. Постукивание по указательному пальцу от основания пальца до его среднего сустава — будет являться надбавкой половины (1/2) от предложенной цены, или 1/4, или 1/8. Если перед указанием дробной степени указывается целое число, то оно умножается на дробную степень.”
Увы, “пять” ни в одной из этих систем не похоже на соответствующий письменный знак. Зато, например, китайцы и сейчас намекают на иероглифы для соответствующих цифр, когда показывают количество на пальцах.
От одного до пяти они считают так же, как мы (начиная с указательного пальца), за тем исключением, что 3 обычно показывают не указательным, средним и безымянным пальцем, а знаком “окей”.
Но самое веселье начинается потом.
Скрещенные пальцы (средний и указательный) при загнутых остальных – Ещё один вариант цифры 10, встречающийся и в Китае, и в Японии. Отсылает, конечно, к тому же иероглифу 十.
И даже если считать простым загибанием пальцев – обратите внимание, что в одной и той же России можно делать это двумя способами: считая загнутые пальцы – или выпрямленные.
Интересно, что каждая система счёта на пальцах кажется пользователям совершенно логичной и разумной, но чем больше таких систем брать, тем больше в них различий. Например, если добавить в эту картину ещё и жестовые языки, то этот знак:
в русском жестовом будет по-прежнему означать 3, а в американском жестовом – уже шесть. А вот китайский жестовый полностью унаследовал все жесты для цифр из обычной китайской традиции.
Из современных систем пальцевого счёта можно упомянуть ещё двенадцатеричную систему, которую продвигают, в частности, два общества, агитирующие за полный переход к двенадцатиричной системе (Dozenal Society of America и Dozenal Society of Great Britain). Аналогичных обществ в других странах мне не известно.
Идея состоит в том, что разным фалангам на пальцах одной руки присваиваются значения, и на эти фаланги можно указывать большим пальцем или другой рукой. Вот так выглядит эта двенадцатиречная рука:
При этом на второй руке можно загибать пальцы по числу полных дюжин. Интересно, что такой счёт, по-видимому, использовался средневековыми новгородцами. Есть версия, что и древними шумерами тоже, но аргумент в её пользу обычно приводят всего один: должны же были шумеры как-то считать на пальцах – почему бы не так.
А вот рука для счёта не восьмёрками, как можно было бы подумать, а сороками: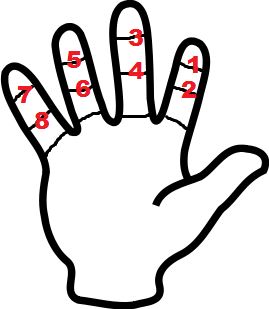
Когда на второй руке оказываются загнуты все пять пальцев по числу полных восьмёрок, в общей сложности получаем 40.
Но самая сложная из подобных систем существовала в Китае, где тоже указывали на фаланги пальцев, но на каждом пальце были места для девяти цифр, и каждый палец сответствовал разряду. Например, указательный означал единицы.
Чтобы показать 3075 в этой системе, нужно было указать большим пальцем на нужные места мизинца, среднего и указательного пальцев.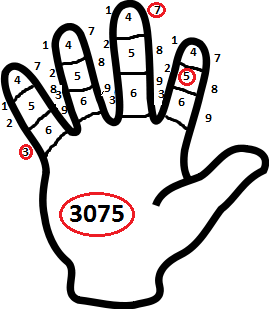
Из новых и ныне здравствующих систем пальцевого счёта стоит назвать бинарную, в которой загнутые и прямые пальцы означают нули и единицы. Такой счёт, понятно, возник с развитием информатики и широко распространён только в узких кругах.
Выглядит это так:
И, конечно, существует множество мнемонических приёмов, позволяющих на пальцах умножать однозначные и двузначные числа на девять, перемножать числа от 6 до 9, переводить из десятичной системы в двоичную и делать много прочего интересного.
Покажите мне рукой цифру 3 – и я что нибудь скажу:)
Вернувшийся из Италии коллега рассказал интересную историю. Он владеет несколькими европейскими языками, читает лекции. В этот раз по Европе, в том числе в Италии, он много ездил “евроэлектричками”. Но рассказ не об этом:).В Италии, в кассе, коллега заказывает три билета. Из-за шума кассир-итальянец переспрашивает: “Синьор заказывает два билета?”. Коллега говорит и показывает “на пальцах” (по итальянски иначе не скажешь:) – три.
Кассир “О, синьор с Украины”. Итальянец рассмотрел Украину в том, как коллега показал цифру 3 – он показал “три”, выпрямив указательный, средний и безымянный палец. В Украине это ещё и символ “малого герба” – тризуба.
Итальянец бы показал цифру “три” большим, указательным и средним пальцем.
Вот теперь вопрос к Вам – как Вы изобразили 3?
Проверил на коллегах. Работает. Немец (гражданин Германии), не задумываясь, показал тройку большим, указательным и средним пальцем.
Кое-что знающий интернет рассказывает по теме много интересного. Прежде всего, пальцы – самый первый счётный инструмент древнего человека. Счет на пальцах – основа десятеричной системы исчисления. И не только. Ведь есть еще фаланги пальцев, есть и традиции, когда считают четверками, потому что большой палец не считался у некоторых. Получаем и другие системы исчисления.
Но сейчас речь прежде всего про отображение цифр жестами, эта тема попроще и в чем то является выжимкой из пальцевого счета. Пальцевый счет местами еще сохранился и даже используется в тех же торговых операциях.
Итак, счет – мы считаем на пальцах, жесты – мы показываем на пальцах.
Китайский метод счёта (речь про счет, а не жесты, и возможны варианты):
0 — сложенный кулак;
1 — выпрямлен указательный палец;
2 — растопырены указательный и средний пальцы;
3 — растопырены указательный, средний и безымянный пальцы;
4 — кроме прижатого к ладони большого пальца, остальные растопырены;
5 — открытая ладонь;
6 — выпрямлены мизинец и большой палец, остальные — сжаты в кулак;
7 — большим палец вместе с указательным и средним сложены в щепоть;
8 — выпрямлены указательный и большой пальцы, остальные — сжаты в кулак;
9 — указательный и большой изогнуты в виде буквы «С», остальные — сжаты в кулак;
10 — три варианта:
– рука сжимается в кулак;
– указательные пальцы обеих рук пересекаются;
– выпрямленный средний палец заводится за выпрямленный указательный, остальные — сжаты в кулак.
В Японии счёт начинается с открытой ладони. Поджатый большой палец представляет число 1, мизинец является числом 5. Таким образом, пальцы, сложенные в кулак – число 5. Затем совершается обратное действие: число 6 обозначается разжатым мизинцем. Возврат к открытой ладони означает число 10.
В виде жестов используется тот же порядок, что в английской или русской традиции: выпрямленный указательный палец становится номером 1, большой палец теперь представляет число 5. Для чисел свыше пяти соответствующее количество выпрямленных пальцев другой руки прижимаются к раскрытой ладони первой. Например, число 7 отображают указательный и средний палец. Число 10 изображается двумя раскрытыми к собеседнику ладонями.
В англоязычных странах счёт до 5 ведётся разжатием пальцев, первоначально собранных в кулак, начиная с указательного пальца, и продолжается до мизинца (число 4). Выпрямленный большой палец указывает на число 5. Аналогичным образом процесс счёта продолжается на другой руке для чисел от 6 до 10. Например, число 7 указывается открытой ладонью с растопыренными пальцами одной руки и выпрямленным указательным и средним пальцами другой.
Чтобы указать на количество своему собеседнику, коренной житель англоговорящей страны поднимает руку или руки вверх. Например, выпрямленные указательный, средний и безымянный пальцы на поднятой вверх ладони будут означать число 3.
Балканские страны на юго-востоке Европы имеют счёт, схожий с английским.
У народов континентальной Западной Европы, таких, как немцы или французы, выпрямленный большой палец представляет собой начало исчисления (число 1). Затем разжимается указательный палец (число 2) и так далее — до мизинца (число 5).
В некоторых европейских странах, а зачастую и во Франции, альтернативный метод подсчёта проводится путём сгибания пальцев в порядке: большой, указательный, средний, безымянный и мизинец.
Русский, украинский и других постсоветских стран счёт на пальцах до десяти начинается с загибания мизинца левой руки и последовательно ведётся до загнутого большого пальца правой руки.
Когда требуется наглядно показать количество, рука сжимается в кулак и сначала разжимается указательный палец, затем средний, безымянный, мизинец и большой.
Английский писатель Р. Мейсон в книге «А ветер не мог читать» приводит пример из истории Второй мировой войны об японке Сабби, оказавшейся в Индии, принадлежащей тогда Великобритании. Великобритания тогда находилась с Японией в состоянии войны. Когда Сабби представили одному англичанину как китаянку, тот предложил ей сосчитать на пальцах до пяти, после чего обман раскрылся:
«Вы видели как она считает? Загибает один за другим пальцы. Вы когда-нибудь видели, чтобы китаец при счёте загибал пальцы? Никогда! Китайцы считают так же, как и англичане. Они поднимают кулак и разгибают пальцы! Она японка!»
В велосипедной гонке «Тур де Франс», перед стартом используется обратный отсчёт от 5 до 1 на пальцах поднятой руки судьи, где 5 – выпрямлены (разжаты) все пальцы, включая большой; 4 – кроме большого, все пальцы выпрямлены; 3 – выпрямлены большой, указательный и средний палец; 2 – выпрямлены указательный и средний палец; 1 – выпрямлен большой или указательный палец; 0 – все пальцы вытянуты снова, но рука отводится в сторону. Это сигнал о начале гонки.
бинарных пальцев!
Забудьте о подсчете до 10 на пальцах … вы можете сосчитать более 1000, если хотите!
Правая рука
Правой рукой вы можете считать до 31:
… и продолжить модель:
|
На самом деле вы рассчитываете в двоичном:
| номер | Сделано | |||||
| 1 | 1 | до | ||||
| 2 | 2 | до | ||||
| 3 | 2 + 1 | до | до | |||
| 4 | 4 | до | ||||
| 5 | 4 + 1 | до | до | |||
| 6 | 4 + 2 | до | до | |||
| 7 | 4 + 2 + 1 | до | до | до | ||
| 8 | 8 | до | ||||
| 9 | 8 + 1 | до | до | |||
| 10 | 8 + 2 | до | до | |||
| 11 | 8 + 2 + 1 | до | до | до | ||
| 12 | 8 + 4 | до | до | |||
| 13 | 8 + 4 + 1 | до | до | до | ||
| 14 | 8 + 4 + 2 | до | до | до | ||
| 15 | 8 + 4 + 2 + 1 | до | до | до | до | |
| 16 | 16 | до | ||||
| 17 | 16 + 1 | до | до | |||
| и т. Д…. | ||||||
Вот еще несколько примеров:
| 16 + 8 + 2 составляет 26 |
| 16 + 8 + 4 + 2 составляет 30 |
Почему?
Таким образом, вы можете рассчитывать на большее число, когда у вас нет карандаша или бумаги.
Вы также можете «запоминать» цифры, правильно держа пальцы.
Или вы можете показать кому-то секретный номер, используя только свою руку (или руки, см. Позже).
Твоя очередь
Практикуйте подсчет от 0 до 31 на пальцах, как и выше.
Делай это много раз, пока не станет легко.
Когда вы можете сделать это хорошо, продемонстрируйте это своим друзьям!
Левая рука
Хотите большие цифры? Ваша левая рука может помочь:
Теперь мы можем использовать все 10 пальцев, чтобы сделать числа, подобные этим:
| 32 + 2 составляет 34 |
| 32 + 16 + 8 + 4 составляет 60 |
| 512 + 256 + 32 + 2 + 1 составляет 803 |
И, наконец, что происходит, когда все пальцы подняты?
| 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 составляет 1 023 |
Итак, теперь вы можете сосчитать только 1000, используя всего 10 пальцев.Вот это да.
Практикуйте это в течение следующих нескольких дней … вы приобретете новый навык, а также обнаружите, что двоичный код гораздо легче понять.
,Touch Урок 6: цифры | Как набрать
Touch Урок 6: цифры
Если вы программируете, работаете с электронными таблицами или часто работаете с числовыми данными, этот урок окажется вам особенно полезным.
7 и 8
Первые две цифровые клавиши, которые мы выучим: 7 8
Чтобы ввести 7 , используйте указательный палец правой руки, чтобы нажать клавишу над и слева от клавиши u .Клавиша 8 набирается средним пальцем правой руки, доходящим вверх и слева от клавиши i .
Печатание Упражнение 6.1777 777 777 777 888 888 888 888 j7j j7j j7j k8k k8k k8k k8k 7j7 7j7 7j7 7j7 8k8 8k8 8k8 8k8 777 JJJ 777 JJJ 888 KKK 888 KKK 787 787 787 878 878 878 7 7 7 7 8 8 8 8 77 77 77 88 88 88 78 78 78 87 87 87 j7j j7j k8k k8k 777 777 777 888 888 888
9 и 0
Сейчас мы научимся печатать: 9 0
Введите клавишу 9 , используя правый безымянный палец, чтобы достичь над и слева от клавиши o .Для клавиши 0 пройдите выше и слева от клавиши p .
Печатание Упражнение 6.2999 999 999 999 000 000 000 000 199 1919; 0; ; 0; ; 0; ; 0; 9l9 9l9 9l9 9l9 0; 0 0; 0 0; 0 0; 0 999 III 999 000 000 ;;; 000 ;;; 909 909 909 090 090 090 9 9 9 9 0 0 0 0 99 99 99 00 00 00 90 90 90 09 09 09 199 19; 0; ; 0; 999 999 999 000 000 000
4 и 3
Давайте теперь изучим некоторые левые клавиши. Начнем с: 4 3
Левый указательный палец используется для ввода клавиши 4 .Доберитесь до и слева от клавиши r , чтобы добраться до нее. Чтобы ввести 3 , используйте левый средний палец, чтобы подняться вверх и влево от e .
Печатное Упражнение 6.3444 444 444 444 333 333 333 333 f4f f4f f4f d3d d3d d3d d3d 4f4 4f4 4f4 4f4 4f4 3d3 3d3 3d3 3d3 444 fff 444 fff 333 ddd 333 ddd 434 434 434 343 343 343 4 4 4 4 3 3 3 3 44 44 44 33 33 33 43 43 43 34 34 34 f4f f4f d3d d3d 444 444 444 333 333 333
2 и 1
Хорошая работа! Вы охватили более половины номеров! Следующие два, чтобы учиться: 1 2
Клавиша 2 набирается левым безымянным пальцем.Он расположен выше и слева от клавиши w . Наберите 1 пальцем мизинца, потянувшись вверх и влево от клавиши q . Это должно быть легко для вас, так как вы научились вводить эту клавишу на последнем уроке, когда набираете ! символов. Разница в том, что для ввода 1 вы не используете смену
Печатание Упражнение 6.4222 222 222 222 111 111 111 111 s2s s2s s2s a1a a1a a1a a1a 2s2 2s2 2s2 2s2 1a1 1a1 1a1 1a1 222 sss 222 sss 111 aaa 111 aaa 212 212 212 121 121 121 2 2 2 2 1 1 1 1 22 22 11 11 11 11 21 21 21 12 12 12 s2s s2s a1a a1a 222 222 222 111 111 111
5 и 6
Почти готово! Последние два числа, чтобы научиться печатать: 5 6
Клавиши 5 и 6 набираются левым указательным пальцем.Клавиша 5 расположена над и справа от клавиши r . Клавиша 6 немного растянута – она находится над и справа от клавиши t .
Печатание Упражнение 6.5555 555 555 555 666 666 666 666 f5f f5f f5f f5f f6f f6f f6f f6f 5f5 5f5 5f5 5f5 6f6 6f6 6f6 6f6 555 ррр 555 ррр 666 ттт 666 ттт 655 6 5 5 6 6 6 6 6 6 6 6 6 6 6 6 5 5 6 6 5 6 6 5 5 6 5 5 6 5 5 6 5 5 6 6 6 6 6 55 55 55 66 66 66 56 56 56 65 65 65 f5f f5f f6f f6f 555 555 555 666 666 666
Подводя итоги
Fantabulous! Теперь вы можете нажать любой номер! Давайте соберем все вместе и проверим ваши новые навыки набора номера: 1 2 3 4 5 6 7 8 9 0
Печатание Упражнение 6.6111 111 111 222 222 222 333 333 333 444 444 444 555 555 555 666 666 666 777 777 777 888 888 888 999 999 999 000 000 000 101 101 292 292 383 383 474 474 565 565 656 656 747 747 838 838 929 929 010 010 123-456-7890 123-456-7890 1.09 8.23 74.56 6.32 98.1 -403.78 45/7 -.9999 / 3
Не стесняйтесь повторять любое из упражнений этого урока. Когда вы сможете выполнить их с почти 100% точностью, вы готовы перейти к следующему уроку!
Следующий урок: символы
,Удобные для ввода числовые значения с `inputmode`
Формы часто являются кошмаром на мобильном телефоне. Мы можем сделать процесс максимально безболезненным, реагируя на контекст . Поля ввода, которые ожидают числовые значения, должны иметь числовой пользовательский интерфейс . Поднять цифровую клавиатуру на маленьких экранах легко на большинстве платформ – просто используйте .
Эта цифровая клавиатура с большими кнопками удобна для пальцев и поможет предотвратить отскок пользователей от вашей формы в отчаянии.Однако type = "number" не подходит для всех номеров .
На (большинстве) больших экранах ввод чисел осуществляется с помощью кнопки увеличения / уменьшения. Это полезный интерфейс, который мы получаем бесплатно по умолчанию. Это, однако, делает этот вид ввода совершенно неуместным, например, для номера кредитной карты.
Интерфейс по умолчанию для ввода чисел выглядит примерно так во всех браузерахСама спецификация проясняет это.
Тип
= числоне подходит для ввода, который состоит только из чисел, но не является строго говоря числом. Например, это не подходит для номеров кредитных карт или почтовых индексов США. Простой способ определить, следует ли использоватьtype = number, состоит в том, чтобы рассмотреть, имеет ли смысл для элемента управления вводом иметь интерфейс spinbox (например, со стрелками «вверх» и «вниз»). Неправильное ошибочное определение номера кредитной карты на 1 в последней цифре – это так же неправильно, как и неправильное получение каждой цифры.Поэтому для пользователя не имеет смысла выбирать номер кредитной карты с помощью кнопок «вверх» и «вниз». Если интерфейс Spinbox не подходит,type = text, вероятно, является правильным выбором (возможно, с атрибутомpattern).
Легко скрыть кнопки вверх и вниз с помощью CSS:
input [type = "number"] {
-мож-внешний вид: текстовое поле;
}
входной [тип = "число"] :: - WebKit-внутренн-спин-кнопку,
input [type = "number"] :: - webkit-external-spin-button {
внешний вид: нет;
поле: 0;
} Важно отметить , что это
.Где должны быть пальцы на клавиатуре?
Обновлено: 24.01.2008 по Computer Hope
Пальцы левой руки должны быть расположены над клавишами A, S, D и F, а пальцы правой руки должны быть над J, K, L и; ключи. Эти ключи считаются ключами домашней строки. Ваши большие пальцы должны или находиться в воздухе или очень легко касаться клавиши пробела.
Какими пальцами нажимать каждую клавишу на клавиатуре?
В приведенной ниже таблице перечислены клавиши домашней строки в верхней синей полосе и каждая клавиша, которую нажимает палец, и клавиши, которые нажимает большой палец (пробел).Как видно из таблицы, оба мизинца, особенно правый мизинец, отвечают за большинство клавиш на клавиатуре.
| A | S | D | F | J | К | л | ; | Пробел |
|---|---|---|---|---|---|---|---|---|
| ~ ` ! 1 Tab Q Caps A Сдвиг влево Слева Ctrl Z Клавиша Fn | @ 2 Вт S X | # 3 E D C | $ 4 % 5 R T F G V B | ^ 6 & 7 Y U H J N M | * 8 I K <, | (9 O L >. | ) 0 Р ; : ? / – _ [{ “‘ Сдвиг вправо + = ]} Удалить \ | Введите Право Ctrl | Alt ключи Windows ключ Дополнительный ключ |
Остальные клавиши клавиатуры, не перечисленные выше, не обязательно назначаются определенному пальцу для их нажатия. Вместо этого вы можете использовать любой палец, который удобнее или удобнее для достижения и нажатия этих клавиш.
ЗаметкаДля клавиш с двумя или более символами вам может потребоваться использовать две руки и два пальца для создания символа.Например, с помощью клавиш скобки и скобки ([{и]}), чтобы набрать фигурную скобку, сначала вы должны нажать левую клавишу Shift левой мизинцем. Затем нажмите клавишу открывания или закрывания скобки правой мизинец.
Сколько пальцев должно быть в домашнем ряду?
В домашнем ряду четырьмя пальцами обеих рук должно быть восемь пальцев.
Должны ли мои ладони отдыхать или они должны быть подняты?
При наборе текста ладони должны быть подняты и не лежать на какой-либо поверхности, в том числе на запястье, и находиться под углом от 10 до 30 градусов.Слишком сильное поднятие или опускание запястий в любом направлении или отдых их во время набора текста может вызвать стресс и привести к синдрому запястного канала.
Прочие советы по безопасности клавиатуры
Во время набора текста держите ладони поднятыми, но есть и другие советы, которые помогут вам избежать запястного канала и боли во время печати. Помните следующие предложения каждый раз, когда вы печатаете.
- Поддерживайте высоту ряда строк клавиатуры как можно ближе к уровню локтя.
- Центрируйте пробел своим телом.
- Не наклоняйте и не сгибайте запястья. Во время набора текста держите запястья поднятыми и максимально прямыми.
- Старайтесь не набирать тексты, так как это вызывает напряжение на шее от необходимости часто смотреть на клавиатуру.
- Не нажимайте больше, чем нужно, чтобы нажимать клавиши.
- Когда вы не печатаете, убедитесь, что вы положили руки и руки. Однако никогда не кладите руки, кисти или запястья на острые края.
- Делайте перерыв в наборе текста каждые 20-30 минут.Если вам трудно вспомнить, когда нужно сделать перерыв, установите таймер или выпейте много воды, вынуждая вас чаще ходить в ванную.
