Что символизируют волны — eta-dzeta.ru
Волна – символ древний, как и само море, считающееся колыбелью жизни. Волны символизируют воду непосредственно, а вода является одним из самых универсальных символов, и включает множество значений в зависимости от своего состояния.
Содержание
- 1 Символика морской волны
- 2 Волна – символ вечного движения
- 3 Волна — символ эмоционального подъема
- 4 Волны – символ иллюзий
- 5 Волны – символ распространения информации
Символика морской волны
Волна символизирует постоянство непостоянного
Бежит из глубины волна,
И, круто выгнув спину,
О берег плещется она,
Мешая ил и тину…Она и бьётся, и ревёт,
И в грохоте и вое
То вдруг раскинет, то сорвёт
Роскошье кружевное…(Сергей Клычков)
Волна – символ вечного движения
Морские волны символизируют изменения и непостоянство или, если сказать от обратного, постоянные изменения.
Морские волны напоминают нам, что жизнь не стоит на месте, все движется и развивается в своем ритме.
Волна символизирует непрерывное изменение материального мира: волны смывают, очищают, наносят песок, меняют форму скал и ландшафта, шлифуют камни и все, что попадает к ним. В этом аспекте можно говорить о том, что волны символизируют трансформацию, независимую от желания объекта. Со временем объект будет изменен так или иначе от взаимодействия с водой.
Гранитные скалы Сейшельских островов оттачивались морскими волнами и ветром в течение столетий
Волны являют собой постоянно движущуюся воду, в которой нет статики, а потому образ волн становится символом вечного движения, никогда не прерывающегося и не прекращающегося. Здесь можно говорить, что волны также символизируют неустанный труд, преобразующий действительность.
Волна может выступать предвестником сильных волнений и надвигающихся изменений.
Также волны могут символизировать быстротечность человеческой жизни, захваченную и поглощенную житейским морем забот.
Волна — символ вечного движения. Фотография Пьера Карро
Волна — символ эмоционального подъема
Вода олицетворяет эмоции, чувствительность, а также движение подсознательных процессов. Волны – это символ большой энергии и высокого эмоционального подъема, на котором можно свершить многое из задуманного. Волны символизируют проявленные эмоции большой силы, хотя их причины могут быть как осознанны, так и нет.
Волна символизирует успех и признание. Выражение «быть на гребне волны» говорит о том, что человек обрел успех, удерживает его и развивает.
Волна также выступает символом самореализации и умения использовать шанс. «Поймать свою волну» — это о нахождении своего дела, проекта, пути, об умении быть в нужном месте в нужное время и не упускать открывшиеся возможности.
В негативном аспекте волна может означать тщеславие от достигнутых высот, а также излишнее возбуждение от самолюбования.
Иногда волны, особенно волны прибоя, могут символизировать неспокойное состояние духа и разума, а также хаотичность мыслей и чувств, захлестнувших человека.
Это не всегда плохо, так как для разрушения старого и высвобождения запертой энергии иногда необходимо великое волнение.
Вода символизирует эмоции. Волны прибоя могут означать сильное душевное волнение и беспокойство
Волны – символ иллюзий
Воде в целом присуща символика, связывающая ее с иллюзиями и иллюзорным восприятием действительности: вода преломляет свет и искажает изображение.
Волны же сами по себе являются явлением иллюзорным для человеческого восприятия. Под воздействием ветра часть поверхности воды прогибается, а часть, наоборот, поднимается вверх. При этом волнение передается другим точкам и захватывает все большую площадь водяной поверхности. И вот наши глаза уже видят некий горизонтальный эффект в виде бегущих волн, но при этом сама вода никуда не перемещается, также, как например колоски ржи в поле, нагибаемые ветром. Мы же видим волну и движение, что, в общем-то, есть некий обман зрения.
Волна — символ иллюзий
Волны – символ распространения информации
Волна символизирует распространение информации, новостей, молвы, при чем, очень быстрое и способное в короткий срок охватывать большие массы.
Затрагивая, как уже говорилось выше, соседние участки, волнение распространяется дальше, вовлекая в этот процесс все новые и новые области. Таким образом, символически волны связаны с пропагандой и внедрением каких-либо идей в сознание окружающих. Это перекликается с символикой обновления, изменения существующего порядка вещей и трансформации, присущей волнам. Выражение «пошла волна» иллюстрирует эффект быстрого распространения новостей и тенденций, а также реакции на них вовлеченных в процесс людей, будь то волна в сфере моды, образования, политики или чего-то еще.
В любом случае, что бы ни приносила волна, она всегда будет напоминать о том, что постоянны лишь перемены.
Волна как символ свободы, энергии и бесконечного движения
Издавна волны считаются одним из основных символов моря или океана. К тому же, все мы живем в волновой среде, которая состоит из различных колебаний (звуковых, электромагнитных). Поэтому неудивительно, что волновая тематика в широком смысле этого понятия нашла свое отражение в различных направлениях дизайна (графике, полиграфии, айдентике, оформлении веб-сайтов и т.
д.).
Суть стиля волна и его преимущества
Стиль под названием «волна» подразумевает использование таких основных водных элементов, как волны и капли. Они могут перетекать одна в другую, накладываться друг на друга или пересекаться, создавая гармоничную композицию.
Дизайн в стиле волна сочетает в себе плавность, изящество, красоту и умиротворенность. Потому это идеальный вариант для выигрышного представления бренда с такими корпоративными чертами, как натуральность, гибкость, спокойствие.
Преимущества использования стиля волна в дизайне:
- формирует визуально утонченный образ;
- позволяет создавать непохожие друг на друга дизайны с «изюминкой»;
- в зависимости от заложенного смысла может создавать как ощущение спокойствия и расслабления, так и постоянного движения.
История возникновения стиля волна
Говоря о волнах в дизайне, трудно сказать, когда и где именно возник этот стиль. Кажется, что он пользуется популярностью еще с древних времен, когда человек научился символично изображать различные окружающие его явления природы, в том числе связанные со стихией воды.
А учитывая то, что волновые эффекты продолжают оставаться неотъемлемой частью жизни современного человека и окружающих его процессов, данный тренд можно по праву назвать «вечным».
Особенности стиля волна, для какого бизнеса может использоваться
Как известно, волны передает чувство расслабленности, умиротворения и медитативности. Поэтому, если деятельность вашей компании связана с очищением или доставкой воды, SPA-услугами, защитой окружающей среды, бьюти-продукцией, туризмом, то рассматриваемый стиль будет отличным вариантом.
Однако, фирменные знаки с элементами волны могут использовать не только те бизнесы, которые напрямую или косвенно связаны с водой. Это могут быть и компании, специализирующиеся на продаже либо производстве электронных приборов или электрического оборудования (поскольку иногда волны обозначают звуковые или электромагнитные колебания).
Кроме того, волновую стилистику могут использовать самые разные направления деятельности, где важно подчеркнуть открытость (за счет чистоты водной капли) и высокое качество (за счет прозрачности воды).
Основные моменты и советы по использованию стиля волна
Основной цветовой гаммой для дизайна в так называемом водном стиле выступают холодные оттенки — от зеленого до сине-фиолетового. Также характерны голубые и бирюзовые тона. Причем даже возможно использование красных, желтых, оранжевых, лиловых оттенков в качестве одного из цветов градиента без потери формы и сути. Если речь идет о логотипах в стиле волны, то выигрышнее всего они смотрятся на контрастном фоне смежной цветовой гаммы — это усиливает впечатление гармоничности и спокойствия.
Водные элементы используют для заполнения определенных форм, которыми могут быть как геометрические фигуры (чаще всего круг), так и определенные объекты-символы. А надпись на логотипе иногда представляют в виде очертаний, визуально напоминающих волны.
Стиль волна в графическом дизайне и иллюстрациях
«Мягкие» линии применяют не только в оформлении фона, но и в качестве иллюстраций.
При их разработке могут быть использованы такие приемы, как градиенты и переходы, наложение полупрозрачных цветов.
Также волнистые линии помогают обрабатывать белое пространство. Так, в некоторых дизайн-проектах волны используются для разделения цветного и белого фона. С помощью такого приема удается четко разделить пространство с заголовком от остальной информации, сделав акцент на главном.
Волновые иллюстрации придают дизайну эффект загадочности и необычности. Благодаря этому такие проекты воспринимаются иначе, нежели те, в оформлении которых использованы прямые линии и прямоугольные фигуры.
Behance @ maruko pum
Стиль волна в айдентике: логотип и фирменный стиль
Основным элементом лого в рассматриваемом стиле всегда является иконка в виде волны. А уже в зависимости от тематики той или иной организации можно использовать самые разные изображения. Гармоничным дополнением водного фирменного знака часто становятся образы рыб и водных млекопитающих, пальм, берегов и скал.
Если речь идет об электрических или звуковых волнах, дизайнеры применяют более абстрактные изображения (например, линии или стилизованные образы морских обитателей).
У воды нет постоянной формы, поэтому как элемент логотипа ее часто изображают в самых разных состояниях: брызг, переливания, текучести, очерчивания того или иного объекта. Это свойство позволяет использовать водные элементы в любых вариациях и фигурах, подобрав то состояние, которое наиболее точно соответствует логотипу вашей компании.
Behance @ studiowmw
Стиль волна в упаковке товаров
Важная особенность волнистых линий состоит в том, что они создают ощущение легкости и безмятежности. Этим они сильно отличаются от прямых линий и жестких форм, которые ассоциируются с некими ограничениями и строгостью, а порой даже с «тяжестью».
Будучи изображенными на упаковках товаров, волны притягивают к себе глаза потребителей, которых на подсознательном уровне интересует все то, что лежит за пределами каких-либо рамок и ассоциируется с чем-то приятным и неотягащающим.
Именно поэтому дизайн в стиле волны можно довольно часто увидеть на этикетках питьевой воды и напитков, упаковках готовых фитнес-завтраков — тех продуктах, которые непосредственно ассоциируются с легкостью и здоровым самочувствием.
Behance @ ADD Branding
Еще волнистые элементы встречаются в дизайне упаковок медицинских препаратов, имеющих жидкую консистенцию (например, капель для глаз, различных растворов и суспензий и т.п.).
Бытовую технику и электронику некоторых брендов, фирменный стиль которых разработан с использованием волновой тематики, также упаковывают в коробки с изображениями водных логотипов.
Стиль волна в веб- и smm-дизайне
Стоит отметить тот факт, что волны и «мягкие» линии постепенно вытесняют четкие и прямолинейные очертания в дизайне сайтов и страниц в соцсетях, становясь одним из самых популярных современных трендов. Такая тенденция обусловлена несколькими причинами:
-
во-первых, легкие и воздушные компоненты вызывают широкий спектр эмоций в дизайне;
-
во-вторых, изогнутые линии и волнообразные фигуры можно комбинировать разными способами, что дает большой простор для дизайнерской фантазии.
Часто «волнистость» на сайтах дополнительно подчеркивают крупными элементами либо небольшими кружочками и кляксами. Они выглядят нестрого, но в целом четко и основательно. В результате на готовой интернет-площадке, будь то интернет-магазин, сайт-визитка или корпоративный сайт, полностью отсутствуют острые углы, что придает ей интересный и стильный вид. Таким образом чаще всего оформлены сайты водных комплексов, турагентств и туроператоров.
Примеры использования стиля волна в Украине
Украинские дизайнеры используют стиль волна при разработке логотипов и фирменного стиля для компаний, непосредственно связанных с морской тематикой: фирм по ловле и реализации рыбной продукции, аквапарков, океанариумов и морских курортов. Из примеров — представленная во многих городах Украинысеть туристических агентств «Поехали с нами»,аквапарк «Остров сокровищ» в Кирилловке,банный клуб «Водолей» в Днепре.
В нашей стране волновые фирменные знаки вы можете заметить и на вывесках организаций, далеких от водной тематики: кафе-кондитерских, терапевтических центров, радиостанций.
Все это говорит о востребованности данного стиля и его актуальности в будущем.
Примеры использования стиля волна в мире
Изображения волн и все, что с ними связано, вдохновляют дизайнеров как в Европе, так и в США на создание дизайна для различных сфер бизнеса и не только. Даже если речь идет о серьезных проектах, где более уместно использование прямых линий, добавление волнистых позволяет сбалансировать общую концепцию и привнести неповторимую «изюминку».
Например, в стиле волны в холодных оттенках выполнен логотип российского производителя систем автоматического полива Aqua Construction.
Стилизованная волна, выполненная с использованием игры цветов, изображена на фирменном знаке американской некоммерческой организации по поддержке экосистемы Tampa Bay Wave.
В волновой тематике представлен и лого компании Philips — одного из самых известных производителей электроники на мировом рынке. Это как раз тот пример, когда деятельность компании не имеет никакого отношения к воде.
Кроме того, креативные волны выбирают в качестве эмблем современных сервисов и приложений, а также компаний, деятельность которых связана с инновационными технологиями (Smart Network, Google Wave и пр.).
Разработка дизайна в стиле волна: где и по какой цене заказать
Если вам нужен индивидуальный дизайн в стиле волна, вы можете поступить одним из способов: либо нанять дизайнера на фрилансе, либо заказать услугу в специализированной компании. В первом случае это будет стоить от 500 грн в зависимости от вида, сложности и объема работ, во втором — цены стартуют от $20.
Но учтите, что среди фрилансеров не так легко найти профессионалов своего дела, как может показаться на первый взгляд, особенно в сжатые сроки. И если полученный результат вас не удовлетворит, вам вряд ли предоставят другие варианты в рамках оплаченной суммы.
Заинтересованы в качественном результате и не хотите рисковать? Тогда обращайтесь в студию WeLoveBrands! Многолетний опыт работы и фантазия наших дизайнеров позволят создать эффектный водный логотип или фирменный стиль, который будут «работать» на имидж вашего бренда.
Для заказа услуги или получения консультации напишите нам сообщение в онлайн-чате или свяжитесь по телефону.
Волна как символ свободы, энергии и бесконечного движения
Издавна волны считаются одним из основных символов моря или океана. К тому же, все мы живем в волновой среде, которая состоит из различных колебаний (звуковых, электромагнитных). Поэтому неудивительно, что волновая тематика в широком смысле этого понятия нашла свое отражение в различных направлениях дизайна (графике, полиграфии, айдентике, оформлении веб-сайтов и т.д.).
Суть стиля волна и его преимущества
Стиль под названием «волна» подразумевает использование таких основных водных элементов, как волны и капли. Они могут перетекать одна в другую, накладываться друг на друга или пересекаться, создавая гармоничную композицию.
Дизайн в стиле волна сочетает в себе плавность, изящество, красоту и умиротворенность. Потому это идеальный вариант для выигрышного представления бренда с такими корпоративными чертами, как натуральность, гибкость, спокойствие.
Преимущества использования стиля волна в дизайне:
- формирует визуально утонченный образ;
- позволяет создавать непохожие друг на друга дизайны с «изюминкой»;
- в зависимости от заложенного смысла может создавать как ощущение спокойствия и расслабления, так и постоянного движения.
История возникновения стиля волна
Говоря о волнах в дизайне, трудно сказать, когда и где именно возник этот стиль. Кажется, что он пользуется популярностью еще с древних времен, когда человек научился символично изображать различные окружающие его явления природы, в том числе связанные со стихией воды.
А учитывая то, что волновые эффекты продолжают оставаться неотъемлемой частью жизни современного человека и окружающих его процессов, данный тренд можно по праву назвать «вечным».
Особенности стиля волна, для какого бизнеса может использоваться
Как известно, волны передает чувство расслабленности, умиротворения и медитативности.
Поэтому, если деятельность вашей компании связана с очищением или доставкой воды, SPA-услугами, защитой окружающей среды, бьюти-продукцией, туризмом, то рассматриваемый стиль будет отличным вариантом.
Однако, фирменные знаки с элементами волны могут использовать не только те бизнесы, которые напрямую или косвенно связаны с водой. Это могут быть и компании, специализирующиеся на продаже либо производстве электронных приборов или электрического оборудования (поскольку иногда волны обозначают звуковые или электромагнитные колебания).
Кроме того, волновую стилистику могут использовать самые разные направления деятельности, где важно подчеркнуть открытость (за счет чистоты водной капли) и высокое качество (за счет прозрачности воды).
Основные моменты и советы по использованию стиля волна
Основной цветовой гаммой для дизайна в так называемом водном стиле выступают холодные оттенки — от зеленого до сине-фиолетового. Также характерны голубые и бирюзовые тона.
Причем даже возможно использование красных, желтых, оранжевых, лиловых оттенков в качестве одного из цветов градиента без потери формы и сути. Если речь идет о логотипах в стиле волны, то выигрышнее всего они смотрятся на контрастном фоне смежной цветовой гаммы — это усиливает впечатление гармоничности и спокойствия.
Водные элементы используют для заполнения определенных форм, которыми могут быть как геометрические фигуры (чаще всего круг), так и определенные объекты-символы. А надпись на логотипе иногда представляют в виде очертаний, визуально напоминающих волны.
Стиль волна в графическом дизайне и иллюстрациях
«Мягкие» линии применяют не только в оформлении фона, но и в качестве иллюстраций. При их разработке могут быть использованы такие приемы, как градиенты и переходы, наложение полупрозрачных цветов.
Также волнистые линии помогают обрабатывать белое пространство. Так, в некоторых дизайн-проектах волны используются для разделения цветного и белого фона.
С помощью такого приема удается четко разделить пространство с заголовком от остальной информации, сделав акцент на главном.
Волновые иллюстрации придают дизайну эффект загадочности и необычности. Благодаря этому такие проекты воспринимаются иначе, нежели те, в оформлении которых использованы прямые линии и прямоугольные фигуры.
Behance @ maruko pum
Стиль волна в айдентике: логотип и фирменный стиль
Основным элементом лого в рассматриваемом стиле всегда является иконка в виде волны. А уже в зависимости от тематики той или иной организации можно использовать самые разные изображения. Гармоничным дополнением водного фирменного знака часто становятся образы рыб и водных млекопитающих, пальм, берегов и скал. Если речь идет об электрических или звуковых волнах, дизайнеры применяют более абстрактные изображения (например, линии или стилизованные образы морских обитателей).
У воды нет постоянной формы, поэтому как элемент логотипа ее часто изображают в самых разных состояниях: брызг, переливания, текучести, очерчивания того или иного объекта.
Это свойство позволяет использовать водные элементы в любых вариациях и фигурах, подобрав то состояние, которое наиболее точно соответствует логотипу вашей компании.
Behance @ studiowmw
Стиль волна в упаковке товаров
Важная особенность волнистых линий состоит в том, что они создают ощущение легкости и безмятежности. Этим они сильно отличаются от прямых линий и жестких форм, которые ассоциируются с некими ограничениями и строгостью, а порой даже с «тяжестью».
Будучи изображенными на упаковках товаров, волны притягивают к себе глаза потребителей, которых на подсознательном уровне интересует все то, что лежит за пределами каких-либо рамок и ассоциируется с чем-то приятным и неотягащающим. Именно поэтому дизайн в стиле волны можно довольно часто увидеть на этикетках питьевой воды и напитков, упаковках готовых фитнес-завтраков — тех продуктах, которые непосредственно ассоциируются с легкостью и здоровым самочувствием.
Behance @ ADD Branding
Еще волнистые элементы встречаются в дизайне упаковок медицинских препаратов, имеющих жидкую консистенцию (например, капель для глаз, различных растворов и суспензий и т.
п.).
Бытовую технику и электронику некоторых брендов, фирменный стиль которых разработан с использованием волновой тематики, также упаковывают в коробки с изображениями водных логотипов.
Стиль волна в веб- и smm-дизайне
Стоит отметить тот факт, что волны и «мягкие» линии постепенно вытесняют четкие и прямолинейные очертания в дизайне сайтов и страниц в соцсетях, становясь одним из самых популярных современных трендов. Такая тенденция обусловлена несколькими причинами:
-
во-первых, легкие и воздушные компоненты вызывают широкий спектр эмоций в дизайне;
-
во-вторых, изогнутые линии и волнообразные фигуры можно комбинировать разными способами, что дает большой простор для дизайнерской фантазии.
Часто «волнистость» на сайтах дополнительно подчеркивают крупными элементами либо небольшими кружочками и кляксами. Они выглядят нестрого, но в целом четко и основательно. В результате на готовой интернет-площадке, будь то интернет-магазин, сайт-визитка или корпоративный сайт, полностью отсутствуют острые углы, что придает ей интересный и стильный вид.
Примеры использования стиля волна в Украине
Украинские дизайнеры используют стиль волна при разработке логотипов и фирменного стиля для компаний, непосредственно связанных с морской тематикой: фирм по ловле и реализации рыбной продукции, аквапарков, океанариумов и морских курортов. Из примеров — представленная во многих городах Украинысеть туристических агентств «Поехали с нами»,аквапарк «Остров сокровищ» в Кирилловке,банный клуб «Водолей» в Днепре.
В нашей стране волновые фирменные знаки вы можете заметить и на вывесках организаций, далеких от водной тематики: кафе-кондитерских, терапевтических центров, радиостанций. Все это говорит о востребованности данного стиля и его актуальности в будущем.
Примеры использования стиля волна в мире
Изображения волн и все, что с ними связано, вдохновляют дизайнеров как в Европе, так и в США на создание дизайна для различных сфер бизнеса и не только.
Даже если речь идет о серьезных проектах, где более уместно использование прямых линий, добавление волнистых позволяет сбалансировать общую концепцию и привнести неповторимую «изюминку».
Например, в стиле волны в холодных оттенках выполнен логотип российского производителя систем автоматического полива Aqua Construction.
Стилизованная волна, выполненная с использованием игры цветов, изображена на фирменном знаке американской некоммерческой организации по поддержке экосистемы Tampa Bay Wave.
В волновой тематике представлен и лого компании Philips — одного из самых известных производителей электроники на мировом рынке. Это как раз тот пример, когда деятельность компании не имеет никакого отношения к воде.
Кроме того, креативные волны выбирают в качестве эмблем современных сервисов и приложений, а также компаний, деятельность которых связана с инновационными технологиями (Smart Network, Google Wave и пр.).
Разработка дизайна в стиле волна: где и по какой цене заказать
Если вам нужен индивидуальный дизайн в стиле волна, вы можете поступить одним из способов: либо нанять дизайнера на фрилансе, либо заказать услугу в специализированной компании.
В первом случае это будет стоить от 500 грн в зависимости от вида, сложности и объема работ, во втором — цены стартуют от $20.
Но учтите, что среди фрилансеров не так легко найти профессионалов своего дела, как может показаться на первый взгляд, особенно в сжатые сроки. И если полученный результат вас не удовлетворит, вам вряд ли предоставят другие варианты в рамках оплаченной суммы.
Заинтересованы в качественном результате и не хотите рисковать? Тогда обращайтесь в студию WeLoveBrands! Многолетний опыт работы и фантазия наших дизайнеров позволят создать эффектный водный логотип или фирменный стиль, который будут «работать» на имидж вашего бренда. Для заказа услуги или получения консультации напишите нам сообщение в онлайн-чате или свяжитесь по телефону.
Обозначение— разница между «≈», «≃» и «≅»
Вопрос задан
Изменено 2 года назад
Просмотрено 305 тысяч раз
$\begingroup$
В математической нотации, каковы различия в использовании между различными приблизительно равными знаками “≈”, “≃” и “≅”?
Стандарт Unicode перечисляет их все в блоке математических операторов.
- ≈ : ПОЧТИ РАВНО (U+2248)
- ≃ : АСИМПТОТИЧЕСКИ РАВНО (U+2243)
- ≅ : ПРИБЛИЗИТЕЛЬНО РАВНО (U+2245)
- обозначение
- приближение
$\endgroup$
9
$\begingroup$
Обозначения $\cong$ и $\simeq$ не полностью стандартизированы. Оба обычно используются для «изоморфных», что означает «одинаковые в любом контексте». Например, «геометрически изоморфный» обычно означает «конгруэнтный», «топологически изоморфный» означает «гомеоморфный» и так далее: это означает, что они каким-то образом «одинаковы» для рассматриваемой вами структуры, в некотором смысле они «эквивалентны, », хотя и не всегда «равные»: у вас могут быть два конгруэнтных треугольника в разных местах на плоскости, поэтому они не будут буквально «одинаковыми», но их внутренние свойства будут одинаковыми.
$\приблизительно$ используется в основном в терминах численных приближений, что означает, что значения в вопросах “близки” друг к другу в любом контексте, в котором вы работаете, и часто менее точно, насколько именно “близко”. Топологи также имеют тенденцию использовать $\приблизительно$ для гомеоморфных.
Основной вывод из этого ответа: нотация не всегда стандартизирована, и важно убедиться, что вы понимаете, в каком бы контексте вы ни работали.
4
$\begingroup$
$\приблизительно используется в основном для приблизительного (читай: вычисленного) значения математического выражения типа $\pi \приблизительно 3.
14$ В LaTeX оно кодируется как \приблизительно.
$\cong$ используется, чтобы показать соответствие между двумя математическими выражениями, которые могут быть геометрическими, топологическими, а при использовании арифметики по модулю вы можете получить разные конгруэнтные числа, например, $5 mod 3 \cong 11 mod 3$ ( хотя это также пишется как $\equiv$). В LaTeX он закодирован как \cong.
$\sim$ — это подобие в геометрии, и его можно использовать, чтобы показать, что две вещи асимптотически равны (они становятся более равными, когда вы увеличиваете переменную вроде $n$). Это более слабое утверждение, чем два других. В LaTeX он кодируется как \sim.
$\simeq$ — это скорее набор значений. В LaTeX он кодируется как \simeq, что означает «похожий равный», поэтому может быть и тем, и другим, что может быть уместно в определенных ситуациях.
$\endgroup$
2
$\begingroup$
≈ для числовых данных, гомеоморфизм
≃ для гомотопической эквивалентности
≅ для изоморфизма, конгруэнтности и т.
д.
Это просто мои собственные соглашения.
$\endgroup$
$\begingroup$
В моей работе “=” – это тождество числа, поэтому оно устанавливает эквивалентность. 1=1, 2х=10, т.е. х=5.
Знак аппроксимации “≈” я использую для десятичной аппроксимации, тильда “~” является более грубой аппроксимацией.
Тильда “~” Я использую, чтобы указать, что геометрическая фигура подобна другой, т.е. треугольник со сторонами 3/4/5 подобен треугольнику со сторонами 30/40/50. Я пишу ▲ABC ~ ▲A’B’C’, где ▲A’B’C’ — расширенная версия прообраза.
Для более близкого сходства “≃” может означать почти конгруэнтный треугольник, но только ПРИБЛИЗИТЕЛЬНО похожий, например, два треугольника 3/4/5 и 3,1/4,1/5,1, а “≅” означает конгруэнтность. Реальные треугольники используют приближения и имеют ошибки округления. 3/4 не равно 3,1/4,1, но может быть грубым приближением для чего-то уже построенного.
Таким образом, это не популярное использование, и пуристы и строгие профессора математики пренебрегают им, потому что у них нет способа его использовать или дать четкое определение. Вот почему неспециалисты или профессионалы в сфере обслуживания могут свободно исследовать его, а ученые предпочитают что-то более четко определенное, если только не допускаются деформации, как в моем случае.
Треугольник 3/4/5 равен ≅ треугольнику 4/5/3 с той разницей, что поворот меняет координаты углов, но сохраняет угол и длину стороны.
Также я использую символ определения “≡” для определения функций. Самый простой случай: f(x) ≡ y. Я использую его, чтобы указать отношение для нахождения сумм, вместо того, чтобы указывать его как сумму, которую мы получаем, однако его можно использовать для определения эквивалентности. Для квадратичного я бы установил f(x) равным нулю, но не определял бы f(x) как ноль. Я использую ≡ для всех случаев, а не только для непосредственных. Установка f(x) на ноль создает эквивалентность f(x) = 0 для координаты, которую вы пытаетесь решить, но не верно для всех координат, которые можно решить.
$\endgroup$
$\begingroup$
Что касается теории категорий:
Символ ≅ используется для изоморфизма объектов категории и, в частности, для изоморфизма категорий (которые являются объектами CAT ). Символ ≃ используется для эквивалентности категорий. По крайней мере, это соглашение используется в этой книге и большинством теоретиков категорий, хотя оно далеко не универсально в математике в целом.
(Предупреждение 1.3.16, Базовая теория категорий Тома Лейнстера).
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Специальные символы — Гиперучебник по физике
[закрыть]
Таблица стилей
Это условные обозначения, используемые в этой книге.
- Векторные величины ( F , g , v ) написаны полужирным шрифтом с засечками, включая векторные величины, записанные греческими символами ( α , τ , ω ).
- Скалярные величины ( m , K , t ) и скалярные модули векторных величин ( F , g , v ) написаны курсивом, шрифтом с засечками, за исключением греческих символов (α, τ, ω), для которых используется шрифт с прямыми засечками.
- В математических символах используется прямой шрифт с засечками (½, +, √, cos) — за исключением случаев, когда они применяются для расчетов с единицами измерения.
- Единицы написаны прямым шрифтом без засечек (м, Н, ℃), как и математические операции с числами и единицами измерения (7 кг × 10 м/с ÷ 3 с = 23,3 Н).
Символы физических величин и их международных единиц
| символ | количество | символ | Единица СИ |
|---|---|---|---|
| р , р | положение, разделение, радиус, радиус кривизны | м | метр |
| с , с | водоизмещение, расстояние | м | метр |
| θ , φ , | угол, угловое смещение, угловое разделение, угол поворота | рад | радиан |
| х , у , з | декартовы координаты | м | метр |
| х , х , к̂ | декартовых единичных векторов | безразмерный | |
| р , θ, φ | сферические координаты | м, | метр, радиан |
| r̂, θ̂, φ̂ | сферических единичных векторов | безразмерный | |
| р, ф, г | цилиндрические координаты | м, | метр, радиан |
| ρ̂, φ̂, ẑ | цилиндрических единичных векторов | безразмерный | |
| № | нормальный единичный вектор | безразмерный | |
| т̂ | тангенциальный единичный вектор | безразмерный | |
| ч | высота, | глубинам | метр |
| л, л | длина | м | метр |
| д | расстояние, разделение, толщина | м | метр |
| т | толщина | м | метр |
| Д | диаметр | м | метр |
| С | окружность | м | метр |
| А , А | площадь, площадь поперечного сечения, площадь проекции, площадь поверхности | м 2 | квадратных метров |
| В | том | м 3 | куб. м. |
| т | время, продолжительность | с | секунд |
| Т | период, периодическое время | с | секунд |
| т | постоянная времени | с | секунд |
| ф | частота | Гц | герц |
| ω | угловая частота | рад/с | радиан в секунду |
| символ | количество | символ | Единица СИ |
|---|---|---|---|
| в , в | скорость, скорость | м/с | метров в секунду |
| и , и | ускорение | м/с 2 | метров в секунду в квадрате |
| а в , а в | центростремительное ускорение, центробежное ускорение | м/с 2 | метров в секунду в квадрате |
| г , г | гравитационное поле, ускорение свободного падения | м/с 2 | метров в секунду в квадрате |
| м | масса | кг | килограмм |
| Ф , Ф | сила | Н | ньютон |
| Ж г , | сила тяжести, вес | Н | ньютон |
| Ф Н , | нормальная сила, нормальная | Н | ньютон |
| Ф ф , | 3 3сила трения (статическая, кинетическая) | Н | ньютон |
| мк с , мк к | коэффициент трения (статический, кинетический) | безразмерный | |
| р , р | импульс | кг м/с | килограмм метр в секунду |
| Дж , Дж | импульс | Н с | ньютон секунд |
| Ш | работа | Дж | джоулей |
| Е | энергия, общая энергия | Дж | джоулей |
| К , | кинетическая энергия (поступательная, вращательная) | Дж | джоулей |
| У , | потенциальная энергия (гравитационная, пружинная) | Дж | Дж |
| В г | гравитационный потенциал | Дж/кг | джоулей на килограмм |
| η | эффективность | безразмерный | |
| П | сила | Вт | Вт |
| ω , ω | скорость вращения, скорость вращения | рад/с | радиан в секунду |
| α , α | ускорение вращения | рад/с 2 | радиан на секунду в квадрате |
| τ , τ | крутящий момент | Н·м | ньютон-метр |
| я | момент инерции | кг м 2 | килограмм метр в квадрате |
| л , л | угловой момент | кг м 2 /с | килограмм-метров в секунду |
| х , х | угловой импульс | Н·м·с | ньютон метр секунд |
| к | жесткость пружины | Н/м | ньютонов на метр |
| П | давление | Па | паскалей |
| о | нормальное напряжение | Па | паскалей |
| т | напряжение сдвига | Па | паскалей |
| р | плотность, объемно-массовая плотность | кг/м 3 | килограмм на кубический метр |
| о | удельная массовая плотность, поверхностная массовая плотность | кг/м 2 | килограмм на квадратный метр |
| λ | линейная массовая плотность | кг/м | килограмм на метр |
| Ф Б , | плавучесть, выталкивающая сила | Н | ньютон |
| q м | массовый расход | кг/с | кг в секунду |
| q В | объемный расход | м 3 /с | кубических метров в секунду |
| Ф Д , | сопротивление, аэродинамическое сопротивление, сопротивление воздуха | Н | ньютон |
| К , К Д | коэффициент аэродинамического сопротивления, коэффициент аэродинамического сопротивления | безразмерный | |
| η | вязкость, динамическая вязкость | Па с | паскаль секунда |
| ν | кинематическая вязкость | м 2 /с | квадратных метров в секунду |
| млн лет | число Маха | безразмерный | |
| Ре | Рейнольдс номер | безразмерный | |
| Пт | фроуд номер | безразмерный | |
| Е | модуль Юнга, модуль упругости | Па | паскалей |
| Г | модуль сдвига, модуль жесткости | Па | паскалей |
| К | объемный модуль, модуль сжатия | Па | паскалей |
| ε | линейная деформация | безразмерный | |
| γ | деформация сдвига | безразмерный | |
| θ | объемная деформация | безразмерный | |
| γ | поверхностное натяжение | Н/м | ньютонов на метр |
| символ | количество | символ | Единица СИ |
|---|---|---|---|
| Т | температура | К | кельвин |
| α | линейное расширение, коэффициент линейного теплового расширения | К −1 | обратный градус Кельвина |
| β | объемное расширение, коэффициент объемного теплового расширения | К −1 | обратный градус Кельвина |
| К | тепло | Дж | джоулей |
| с | удельная теплоемкость, удельная теплоемкость | Дж/кг К | джоулей на килограмм-кельвин |
| Л | скрытая теплоемкость, удельная скрытая теплоемкость | Дж/кг | джоулей на килограмм |
| нет | количество вещества | моль | |
| Н | количество частиц | безразмерный | |
| П | расход тепла | Вт | Вт |
| к | теплопроводность | Вт/м К | ватт на метр кельвин |
| ε | Коэффициент излучения | безразмерный | |
| У | внутренняя энергия | Дж | джоулей |
| С | энтропия | Дж/К | джоулей на кельвин |
| ш | путей, количество одинаковых микросостояний | безразмерный | |
| КС | коэффициент полезного действия | безразмерный |
| символ | количество | символ | Единица СИ |
|---|---|---|---|
| λ | длина волным | метров | |
| в , в | скорость волны | м/с | метров в секунду |
| я | интенсивность | Вт/м 2 | Вт на квадратный метр |
| Л | уровень | дБ, | децибел, децибел |
| нет | показатель преломления, абсолютный показатель преломления | безразмерный | |
| ф | фокусное расстояние | м | метр |
| М | увеличение | безразмерный |
| символ | количество | символ | Единица СИ |
|---|---|---|---|
| кв , кв | заряд, электрический заряд | С | кулон |
| р | плотность заряда, объемная плотность заряда | С/м 3 | кулонов на кубический метр |
| о | поверхностная плотность заряда, поверхностная плотность заряда | С/м 2 | кулонов на квадратный метр |
| λ | линейная плотность заряда | С/м | кулонов на метр |
| Ф Э , Ф Э | электрическая сила, электростатическая сила | Н | ньютон |
| Э , Э | электрическое поле | Н/З, В/м | ньютон на кулон, вольт на метр |
| Φ E | электрический поток | Н·м 2 /C, В·м | ньютон-метр в квадрате на кулон, вольтметр |
| У , У Э | потенциальная энергия, электрическая потенциальная энергия | Дж | джоулей |
| В, В Е | напряжение, потенциал, электрический потенциал | В | вольт |
| ℰ | электродвижущая сила, эдс | В | вольт |
| С | емкость | Ф | фарад |
| κ | диэлектрическая проницаемость | безразмерный | |
| я | ток, электрический ток | А | ампер |
| р , р | сопротивление, электрическое сопротивление, внутреннее сопротивление | Ом | Ом |
| р | Удельное сопротивление | Ом·м | Омметр |
| Г | проводимость | С | Сименс |
| о | проводимость | См/м | сименс на метр |
| Ф Б , Ф Б | магнитная сила | Н | ньютон |
| Б , Б | магнитное поле | Т | тесла |
| Φ В | магнитный поток | Вб | вебер |
| Н | количество витков | безразмерный | |
| нет | витков на единицу длины, плотность витков | м −1 | обратный счетчик |
| η | плотность энергии | Дж/м 3 | джоулей на кубический метр |
| С , С | вектор пойнтинга, интенсивность | Вт/м 2 | Вт на квадратный метр |
| символ | количество | символ | Единица СИ |
|---|---|---|---|
| γ | фактор Лоренца, гамма Лоренца | безразмерный | |
| ф | рабочая функция | Дж | джоулей |
| ψ ( r , t ), | волновая функция | безразмерный | |
| Т ½ | период полураспада | с | секунд |
| Д | доза, поглощенная доза | Гр | серый |
| Н | эффективная доза | Св | зиверт |
Разные символы
| символ | описание |
|---|---|
| + | плюс, добавить, положительный |
| − | минус, вычесть, минус |
| ± | неопределенность, ошибка, плюс-минус |
| · | умножение, точка, скалярное произведение, скалярное произведение |
| × | умножение, перекрестное произведение, векторное произведение |
| ÷, / | разделить |
| x 2 | квадрат |
| x 3 | куб |
| √ | квадратный корень, корень, радикал |
| ∛ | кубический корень |
| 1 х , х −1 | обратный, обратный |
| = | равно, равенство |
| ≈ | примерно равно |
| ∝ | пропорционально |
| ≠ | не равно, неравенство |
| ~ | по заказу, тильда |
| < | меньше |
| > | больше |
| ≤ | меньше или равно |
| ≥ | больше или равно |
| ⇒, ⇐ | логическое следствие |
| ⇔ | логическая эквивалентность |
| … | и так далее, многоточие |
| ∴ | поэтому |
| ф ( х ) | функция |
| грех | синус |
| потому что | косинус |
| желто-коричневый | тангенс |
| гиперболический синус | |
| кош | гиперболический косинус |
| танх | гиперболический тангенс |
| х̂ | Единичный вектор, шляпа, циркумфлекс |
| ∥ | параллельно |
| ⟂ | перпендикулярно |
| х | среднее, среднее, античастица, полоса, над чертой |
| х̃ | медиана, суперсимметричная частица, тильда |
| ⟨⟩ | среднее по времени, среднее по ансамблю, скобка |
| р ( х ) | распределение вероятностей, функция плотности вероятности |
| ∆ | приращение, изменение, дельта |
| д | дифференциал, д |
| ∂ | частичный дифференциал, d частичный |
| ∇ | градиент, дел |
| ∇· | расхождение, деление, точка |
| ∇× | завиток, крест |
| ∇ 2 | лапласиан, дель в квадрате |
| ∑ | сумма, сигма |
| ∫ | встроенный |
| ∬ | двойной интеграл |
| ∭ | тройной интеграл |
| ∮ | интегральный контур |
| ∯ | встроенная поверхность |
| ∰ | объемный интеграл |
| ∞ | бесконечность |
| ℵ 0 | трансфинитное число, алеф ноль |
| письмо | Английское имя | письмо | Английское имя |
|---|---|---|---|
| А, а | альфа | Ν, ν | ну |
| В, β, ϐ | бета | Ξ, ξ | и |
| Г, γ | гамма | О, о | омикрон |
| Δ, ∆, δ | дельта | Π, ∏, π, ϖ | пи |
| Ε, ε, ϵ | эпсилон | Ρ, р, ϱ | ро |
| Ζ, ζ | дзета | Σ, ∑, σ, ς | сигма |
| Η, η | эта | Т, т | тау |
| Θ, ϴ, θ, ϑ | тета | Υ, υ | ипсилон |
| Ι, ι | йота | Ф, ф, ф | фи |
| Κ, κ, ϰ | каппа | х, х | Чи |
| Λ, λ | лямбда | Ψ, ф | фунтов на кв. дюйм |
| М, мк, мк | мю | Ом, Ом, Ом | омега |
| символ | небесное тело | символ | созвездие |
|---|---|---|---|
| ☉ | Вс | ♈ | Овен |
| ☿ | Меркурий | ♉ | Телец |
| ♀ | Венера | ♊ | Близнецы |
| ♁ | Земля | ♋ | Рак |
| ☽, ☾ | Луна | ♌ | Лев |
| ♂ | Марс | ♍ | Дева |
| ♃ | Юпитер | ♎ | Весы |
| ♄ | Сатурн | ♏ | Скорпиус |
| ♅, ⛢ | Уран | ♐ | Стрелец |
| ♆ | Нептун | ♑ | Козерог |
| ♇, ⯓ | Плутон | ♒ | Водолей |
| ⚳ | Церера | ♓ | Рыбы |
| символ | имя |
|---|---|
| ♭ | плоский, на полтона ниже |
| ♮ | натуральный, без регулировки полутона |
| ♯ | диез, на полтона выше |
математических символов – список символов, примеры решения
Математика — это числа, символы и формулы.
Математические символы используются для разных целей в разных областях математики. Использование символов для представления математической информации облегчает понимание выражений, поскольку эти символы показывают взаимосвязь между величинами. В этой статье давайте рассмотрим общие, которые мы используем в разных областях математики.
| 1. | Общие математические символы |
| 2. | Константы, используемые в качестве математических символов |
| 3. | Математические символы, используемые в логике |
| 4. | Диаграмма Венна и символы теории множеств |
| 5. | Цифровые символы |
| 6. | Символы геометрии и алгебры |
| 7. | Греческие алфавиты и символы комбинаторики |
| 8. | Решенные примеры |
| 9. | Практические вопросы |
10. | Часто задаваемые вопросы о математических символах |
Общие математические символы
Если мы напишем несколько раз слова «прибавление 4 к 2 дает 6», это может усложнить ситуацию. Эти слова также занимают больше места и требуют времени для написания. Вместо этого мы можем сэкономить время и место, используя символы. Язык и словарный запас математики содержат большое количество символов, и этот список бесконечен — некоторые из них более технические, чем другие. У нас есть как минимум 10 000+ символов, и некоторые из них мы редко используем. Наиболее распространенные символы перечислены в следующей таблице:
| Символы | Значение | Примеры математических символов |
|---|---|---|
| + | Добавить | 5 + 4 = 9 |
| – | Вычесть | 5 – 4 = 1 |
| = | равно | 1+1 = 2 |
| \(\экв\) | Тождественно равно | (а+б) 2 \(\экв\) а 2 + 2аб +б 2 |
| \(\примерно\) | Приблизительно равно | \(\пи \приблизительно 3,14\) |
| \(\neq\) | Не равно | 5 + 4 \(\neq\) 1 |
| \(\раз\) | Умножить | 5 \(\раз\) 4 = 20 |
| \(\дел\) | Разделить | 10 \(\дел\) 2 = 5 |
| \(<\) | Менее | 10 \(<\) 20 |
| \(>\) | Больше | 20 \(>\) 10 |
| \(\leq\) | Меньше или равно | х + у \(\leq\) г |
| \(\geq\) | Больше или равно | х + у \(\geq\) г |
| \(\%\) | Процент | 50% = \(\begin{align}\frac{50}{100}\end{align}\) |
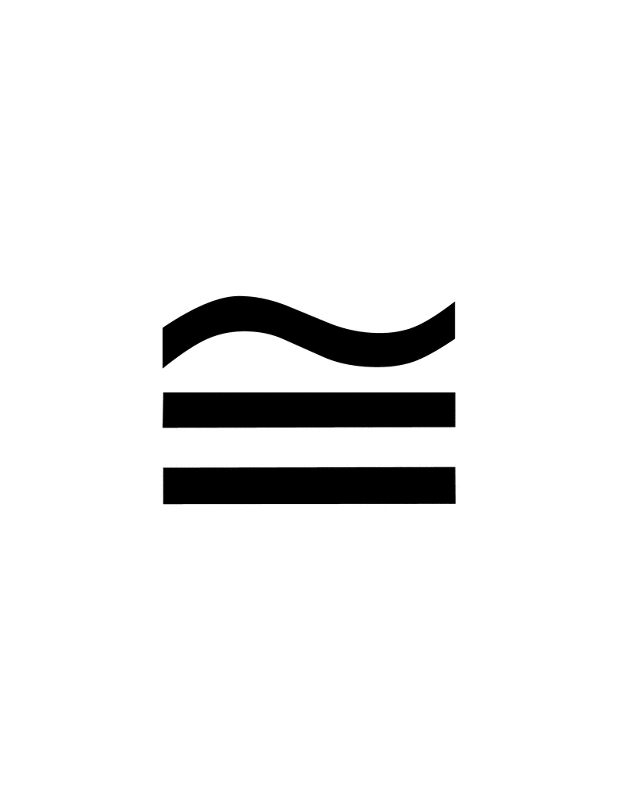\(. \) | Десятичная точка или период | \(\begin{align}\frac{1}{2} = 0,5\end{align}\) |
| \(-\) | Винкулум Разделяет числитель и знаменатель | \(\begin{align}\frac{2}{3}\end{align}\) |
| \(\sqrt{} \) | Квадратный корень | \(\sqrt{4} = 2\) |
| \(\sqrt[3]{х}\) | Кубический корень из x | \( \sqrt[3]{27} = 3\) |
| \( \sqrt[n]{x}\) | n th корень \(x\) | \( \sqrt[4]{16} = 2\) |
| \(()\) | Скобки | \(2+(5-3) = 2 +2 = 4\) |
| \([\:\:]\) | Квадратные скобки | \(\ начало {выравнивания} &3\раз[2 +(5 -2)] +1 \\ &3 \раз[2+3] +1 \\ &3 \times5+1\\ &16 \конец{выравнивание}\) |
| \(\{\}\) | Кронштейн для цветов | \(\begin{выравнивание} &16 \div \{3\times[2 +(5 -2)] +1\} \\ &16 \дел \{3 \раз[2+3] +1\} \\ &16 \дел \{3 \times5+1\}\\ &16 \дел \{16\} \\ &1 \конец{выравнивание}\) |
| \(\в\) | Принадлежит | 0 \(\in\) Целое число |
| \(\нет\в\) | Не принадлежит к | \(\frac{1}{2} \not\in\) Натуральные числа |
| \(\поэтому\) | Поэтому | \(х+1 = 2 \следовательно, х = 1\) |
| \(\потому что\) | Потому что | \(\begin{align}\frac{1}{2} \!\div\! 0,5 \!= \!1 (\потому что\! \frac{1}{2} \!=\! 0,5)\ конец {выравнивание} \) |
| \(\infty\) | Бесконечность | Бесконечность бесчисленна, \(\begin{align}\frac{1}{3}\end{align}\) при записи в десятичной форме, бесконечно \(0,333. |
| \(!\) | Факториал | \( 5!\ \!\!=\! 5 \!\раз\! 4 \!\раз\!3 \!\раз\! 2\! \раз\! 1\) |
….\)Константы, используемые в качестве математических символов
Мы используем константы в математике для обозначения неизменных объектов. Эти константы могут включать в себя ключевые математические наборы, ключевые числа, ключевые математические бесконечности и другие ключевые математические объекты (например, единичную матрицу). Эти математические константы чаще всего принимают форму буквы алфавита или ее производной. В следующей таблице перечислены некоторые наиболее часто используемые константы, а также их имена, значения и использование.
| Имя символа | Пояснение |
|---|---|
| 0 (ноль) | Аддитивная идентичность общих чисел |
| 1 (один) | Мультипликативная идентичность обычных чисел |
| √2 (квадратный корень из 2) | Положительное число, квадрат которого равен 2. Приблизительно равно 1,41421. |
| e (постоянная Эйлера) | Основание натурального логарифма. Предел последовательности (1 + (1/n) n ). Приблизительно равно 2,71828 |
| \(\pi\) (Pi, постоянная Архимеда) | Отношение длины окружности к ее диаметру. Половина окружности единичного круга. Приблизительно равно 3,14159 |
| \( \phi\) (Phi, золотое сечение) | Отношение между большим числом и p меньшим числом q, когда (p+q)/p = p/q. Положительное решение уравнения y 2 -y-1 = 0 . |
| i (Воображаемая единица) | Главный корень из -1. Основной компонент комплексного числа. |
Математические символы, используемые в логике
В следующей таблице показаны математические символы, используемые в логике.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\существует\) | Существует по крайней мере один | ∃ х: Р(х)∃ х: F(х) Существует хотя бы один элемент p(x), \(x\), , такое что F(x) равно True. |
| \(\существует!\) | Существует один и только один | ∃! х: Ф(х) означает, что существует ровно один \(x\) 92 > 1\) |
| \(\отрицательный\) | Логический Не | Утверждение A истинно, только если \(\neg\) ложно \(х \neq y \iff\neg(x=y)\) |
| \(\лор\) | Логическое ИЛИ | Утверждение A \(\lor\) B истинно , если A или B верно; , если оба ложны, утверждение неверно. |
| \(\земля\) | Логический И | Утверждение A \(\land\) B истинно , если A и B оба верны; иначе это ложь. |
| \(\подразумевается\) | подразумевает | х = 2 \(\подразумевается\) x 2 = 4 |
| \(\если\) | Если и только если | х +1 = у +1 \(\ тогда и только тогда) х = у |
| \(\text{|}\) или \(\text{:}\) | Такой, что | { \(х\) | \(х\) > 0} = {1,2,3,. ..} |
Диаграмма Венна и символы теории множеств
В следующей таблице показаны математические символы, используемые в диаграммах Венна и теории множеств.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\крышка\) | Перекресток | А = {2,3,4} Б = {4,5,6} А \(\заглавная\) В = {4} |
| \(\чашка\) | Союз | А = {2,3,4} В = {4,5,6} А \(\чашка\) В = {2,3,4,5,6} |
| \(\ничего\) | Пустой набор | Набор без элементов \(\varnothing\) = { } |
| \(\в\) | Является членом | 2 \(\в\) \(\mathbb{N}\) |
| \(\нотин\) | не является членом | 0 \(\нетин\) \(\mathbb{N}\) |
| \(\подмножество\) | Является подмножеством | \(\mathbb{N} \подмножество \mathbb{I}\) |
| \(\расстроен\) | Является надмножеством | .\(\mathbb{R} \supset \mathbb{W}\) |
| \(\текст{П(А)}\) | Силовой набор А | P({1,2}) = {{}, {1}, {2}, {1,2}} |
| \(А=В\) | Равенство (одинаковые элементы в наборе А и наборе В) | А = {1,2}; В = {1,2} \(\ подразумевает \) А = В |
| \( А \раз В\) | Декартово произведение Набор заказанных пар от A и B | А ={5,6}; В = {7,8} \(\ подразумевает \)\( A \times B\) = {(5,7),(5,8),(6,7),(6,8)} |
| \(\текст{|А|}\) | Количество элементов в множестве A | |{1,2,3,4}| = 4 |
Цифровые символы
Цифровые символы с их примерами и соответствующие индийско-арабские цифры перечислены здесь, в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| Римская цифра I | Значение = 1 | I = 1 , II = 2 , III = 3 |
| Римская цифра V | Значение = 5 | IV = 4 (5-1) ВИ = 6 (5+1) VII = 7 (5+2) VIII = 8 (5+3) |
| Римская цифра X | Значение = 10 | IX = 9 (10-1) |
| Римская цифра L | Значение = 50 | XLIX = 49 (50-1) |
| Римская цифра C | Значение = 100 (столетие) | СС = 200 (100+100) CCLIX = 259 (100+100+50+9) |
| Римская цифра D | Значение = 500 | DCLI = 651 (500+100+50+1) DCCIV = 704 (500+100+100+4) |
| Римская цифра M | Значение = 1000 | ММ = 2000 (1000+1000) |
| R или \(\mathbb{R}\) | Вещественные числа | \(\frac{1}{2} , \frac{1}{4}, 0,5\)\(\sqrt{2},\sqrt{3}\) |
| Z или \(\mathbb{Z}\) | Целое число | -100,-20,5,10,. … |
| N или \(\mathbb{N}\) | Натуральные числа | 1,2,3,…500,… |
| Q или \(\mathbb{Q}\) | Рациональные числа | \(-\frac{1}{2}, \frac{1}{4}, 0,5\) |
| P или \(\mathbb{P}\) | Иррациональные числа | \(\sqrt{2},\sqrt{3}\) |
| C или \(\mathbb{C}\) | Комплексные номера | 5+2i |
Символы геометрии и алгебры
В приведенной ниже таблице показаны наиболее часто используемые геометрические символы. Математические символы с названиями и примерами также приведены в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\угол\) | Укажите угол | \(\угол ABC\) |
| \(\Дельта\) | Символ треугольника | \(\Дельта\текст{PQR}\) |
| \(\конг\) | соответствует | \(\Delta \text{PQR} \cong \Delta \text{ABC}\) 9\цирк\) |
| \(\overline{\rm AB}\) | Отрезок линии AB | Линия из точки А в точку Б |
| \(\overrightarrow{\rm AB}\) | Рэй AB | Линия, начинающаяся от точки А и заканчивающаяся точкой В |
| \(\overleftrightarrow{\rm AB}\) | Линия AB | Бесконечная линия, проходящая через точки A и B | 9в\)
Символы алгебры
В следующей таблице показаны наиболее часто используемые алгебраические символы.
Математические символы с названиями и примерами также приведены в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(х,у\) | Переменные | \(х=5\), \(у=2\) |
| \(+\) | Добавить | \(2x +3x = 5x\) |
| \(-\) | Вычесть | \(3x-x = 2x\) |
| \(.\) | Продукт | \(2x .3x = 6x\) |
| \(-\) | Подразделение | \(\ гидроразрыва {2x}{3y}\) |
| \(\экв\) | Тождественно равно | 92\)|
| \(\neq\) | Не равно | \(a + 5 = b+1 \ подразумевает a \neq b\) |
| \(=\) | равно | \(а = 5\) |
\(\пропто\) | Пропорционально | \(x \propto y \имеется в виду x= ky \) |
| \(f(x)\) | Функция отображает значения \(\)x в \(f(x)\) | \( f(x) = x +3 \) |
Греческие алфавиты и символы комбинаторики
В таблице ниже показаны греческие алфавиты, используемые в качестве математических символов.
Их имена, использование и примеры также перечислены в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\альфа\) | Альфа | Используется для обозначения углов, коэффициентов |
| \(\бета\) | Бета | Используется для обозначения углов, коэффициентов |
| \(\гамма\) | Гамма | Используется для обозначения углов, коэффициентов |
| \(\Дельта\) | Дельта | Дискриминантный символ |
| \(\варепсилон\) | Эпсилон | Используется для обозначения универсального набора | .
| \(\йота\) | Йота | Представляет мнимое число |
| \(\лямбда\) | Лямбда | Представляет константу |
| \(\пи\) | Пи | \(\пи \примерно 3,14\) |
| \(\Сигма\) | Сигма | Представляет собой сумму |
| \(\тета\) | Тета | Представляет углы |
| \(\ро\) | Ро | Статистическая константа |
| \( \фи\) | Фи | Обозначение диаметра |
Символы комбинаторики
В таблице ниже показаны наиболее часто используемые символы комбинаторики.
96{P_4} &= 6 \times 5 \times 4 \times 3 = 360\end{align}
Похожие статьи о математических символах
Ознакомьтесь со следующими страницами, посвященными математическим символам.
- Арифметика
- Алгебраические выражения
- Правила делимости
- Векторы
Важные примечания
Вот несколько моментов, которые следует помнить при изучении математических символов:
- Использование символов для представления информации облегчает понимание математических выражений.
- У нас есть как минимум 10 000+ символов, и некоторые из них мы редко используем.
- Мы используем константы в математике для обозначения неизменяющихся объектов.
Часто задаваемые вопросы о математических символах
Что такое U в математических символах?
Математический символ U используется для обозначения множества, состоящего из элементов двух множеств.
Следовательно, объединение двух множеств P и Q будет множеством элементов P и Q. Для обозначения множества используется специальный символ ∪, который выглядит как «U».
Сколько существует математических символов?
Более 10000 математических символов. Некоторые из основных: =,+,−,≠,±, * и так далее. Есть сложные символы, такие как \(\alpha\), \(\varepsilon\) и так далее.
Какой математический символ используется для обозначения периода волны?
Математический символ, который используется для обозначения периода волны, — λ. Он также известен как длина волны, которая измеряется в единицах расстояния.
Для чего используется математический символ сложения?
Символ сложения (+) обычно используется при сложении двух и более чисел, например, 5 + 5. Кроме того, символ (+) также может использоваться для обозначения положительного числа, например, +7.
Перечислите некоторые распространенные арифметические математические символы.
Некоторые из распространенных арифметических математических символов: знак плюс (+), используемый для сложения, знак минус (-), используемый для вычитания, знак звездочки (*) или знак умножения (×), используемый для умножения, и знак деления (÷).
