Значение символ бесконечности: изучаем символику и происхождение знака

что обозначает знак бесконечности кроме как в математике? – Bomfim Advogados

Содержание

• Тату бесконечность на запястье
• Бесконечность разных размеров
• Кодировка символа бесконечности
• Что означает знак бесконечности на браслете?
• Арабское число 8 и его значение в разных культурах

Знак бесконечности имеет множество значений – это символ мудрости, богатства, внутренней свободы и вечной любви. Стеснительным и нерешительным людям знак бесконечности на красной нити поможет открыть горизонт возможностей, поверить в собственные силы, обрести надежду на положительные перемены в своей жизни. Обязательно поговорите с талисманом, когда будете впервые надевать его, прочитайте соответствующую молитву. В случае с нашими украшениями символ бесконечности обозначает безграничное будущее женщин, спасающихся от торговли людьми. Ожерелье Infinity соответствует всем мотивам Purpose Jewelry и воплощает в себе настоящую надежду и возможности. Символ бесконечности изначально представлял собой не что иное, как фигуру 8.

Кроме того, это ярко выраженное желание человека жить свободно, без всяких ограничений и запретов. В философии этот знак трактовался как неизмеримость или неспособность понять, познать пространство и время. Поэтому не только восьмерка, но и круг также считается символом бесконечности. И если вы будете применять изображение Уробороса в виде круга для активации талисманов фен-шуй, например, таких как чаша богатства, то это ошибкой не будет. В математике символ бесконечности используется для обозначения предела, когда некая переменная достигает любых значений, но никогда не принимает значения, равного бесконечности. Посредством изображения Уроборос (змеи, которая поедала свой собственный хвост) мир искусства передал идею, похожую на бесконечность.

Тату бесконечность на запястье

Обе змеи, за одним исключением, символически занимают место бесконечности ∞. Любящие пары могут использовать украшения (или татуировки) с этим символом, чтобы показать свою неугасающую любовь друг к другу.

В математике этот символ используется как число, но бесконечность не имеет конкретного значения, это просто понятие.

• Металлический символ может быть выполнен с гравировкой в виде имен влюбленных, даты их знакомства или свадьбы, имен детей.
• Она настолько неизведанная и неопределенная, что еще никто не смог узнать, где её начало, а где конец.
• Для них это может означать бесконечную любовь или, наоборот, бесконечное одиночество.
• Этот символ — идеальный подарок для крещения, конфирмации или другой религиозной церемонии.

Все это вы можете напечатать при помощи классических символов на самой обычной клавиатуре. Можете также попробовать изменить раскладку, от этого тоже много зависит. Печатайте нестандартные изображения и удивляйте собеседников, ведь такие знаки используются очень редко и практически не встречаются в классических текстах. Древняя символика всегда играла большую роль в жизни людей, ведь знаки с длительной и загадочной историей, сакральным значением способны придавать сил, энергии, уверенности и веры.

Многие люди воспринимают определенные украшения не просто как часть имиджа, а как личный талисман. Хотя этот магический символ может быть использован и в качестве отдельного талисмана.

Бесконечность разных размеров

Мало кому известно, что происхождение самого знака бесконечности далеко не математическое, намного раньше этот символ использовался еще в тибетских наскальных гравюрах. По легенде этот змей по имени Уроборос, пытался съесть себя, но со временем вырастал и не мог этого сделать, и так продолжалось вечно. Поэтому он стал обозначать начало и конец, и их соединение в естественных циклах. В первую очередь этот символ обозначает вечность бытия, невозможность постичь мир полностью. Например, для верующих людей, это знак непостижимости божеских замыслов, а для философов — символ того, что нельзя измерить понятия пространства и времени, разгадать загадки природы. Очень часто таким значением татуировку наделяют люди науки.

Из смерти рождается жизнь, а из разрушения рождается творение, бесконечный цикл обновления.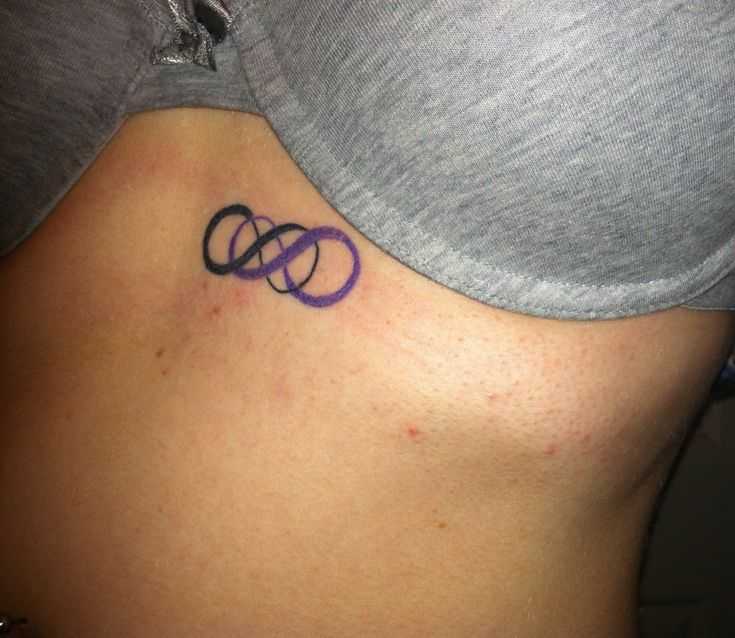 Свои корни знак бесконечности берёт далеко не в математических учениях, а в рисунках, которые были найдены на скалах в Тибете. Ещё тогда знак бесконечности уже начинал обретать свои первые очертания, правда в виде не простого символа, а змеи. Это был образ змея, который стремился проглотить собственный хвост, дабы съесть себя.

Соответственно, подлинно бесконечным Декарт признаёт лишь всемогущего Бога, а такие проявления бесконечности, как «бесконечность человеческой воли», считает проявлениями божественного образа в существе человека. Расположение тату бесконечность для девушек может быть разным. Это не только запястье, пальцы или плечо, но и шея, спина, ребра, грудь, подключичная область, стопа и т.

Этот знак принято использовать для обозначения понятия бесконечности. Неизмеримый параметр был впервые введен в математике в 17 столетии. И хотя мы привыкли связывать символ бесконечности в первую очередь с наукой, у знака, на самом деле, очень древняя и неоднозначная предыстория.

У кельтов также был «кельтский узел», который выглядит как двойной символ бесконечности. Бесконечная природа узла подобна Уроборосу и олицетворяет непреходящую революцию и непрерывность жизни. Эти значения сохранялись на протяжении многих лет, и символ является синонимом выносливости, вечности и возрождения. Знаку бесконечности многие люди придают некое мистическое значение. В школе мы узнали о цифре «8», а ведь именно этот символ олицетворяет собой мистическую силу в культурных традициях многих стран. Для Пифагора древнегреческого мистика и математика число «8» олицетворяло собой стабильность и гармонию.

Кодировка символа бесконечности

Обычно, люди в достаточной степени уверенные в себе, выбирают тату в виде знака бесконечности, что бы подчеркнуть своё стремление к непрерывному развитию, поиску путей достижения совершенства. При этом окружности не в пример вертикальной 8, лежат в одной плоскости, что говорит о том, что в знаке бесконечности подразумевается равенство мужской и женской силы, где два становятся одним. В связи с этим, как и китайский символ дуальной пары инь-ян, символ бесконечности вошел в число многих концепций парности или двойственности. Всем известное арабское число 8, от которого, как считается, произошел знак горизонтальной восьмёрки, является мощнейшим символом у народов многих культур. Швейцарский математик Якоб Бернулли в своей статье опубликовал изображение знака бесконечности, демонстрирующего описанную им плоскую алгебраическую кривую, и назвал его «лемнискатой». Так в Древней Греции именовали специальное крепление в виде бантика для венка, победившего в спортивных состязаниях.

Бесконечность у многих ассоциируется с вечностью, мудростью и тайным знанием. Это не лишено смысла, ведь знание полного значения символики бесконечности поможет с толком использовать тайные знания и, благодаря символу, улучшить свою жизнь. Он характеризуется не вычисляемыми значениями, не имеющие границ или меру. Такой символ впервые применил математик Джон Валлис в 1655 году. Существует множество идей, что вдохновила англичанина именно на такое изображение абсолютной безграничности. Так символ бесконечности — просто математический знак, но с другой стороны он имеет более глубокие значение и даже магическое влияние.

Татуировки могут быть любого размера и находят себе место в самых неожиданных местах, вплоть до живота в области пупка. Даже если у физической Вселенной и существуют границы, у нас все еще есть теория мультивселенной, которая рассматривает существование бесконечного количества Вселенных, в которых могут быть отличные от нашей законы физики. Термин бесконечность соответствует нескольким различным понятиям, в зависимости от области применения, будь то математика, физика, философия, теология или повседневная жизнь. На металлических символах можно выгравировать имена любимых, знакомых, даты свадьбы или детей.

Затем идёт Alt+7 для обозначения точки посередине строчной прописи. При этом удерживая Alt и не отпуская до полного ввода желаемой комбинации. Сколько интересного уже рассказано о ней и сколько неизведанного она таит в себе до сих пор. До этого — цепочка молекул была разомкнута , и что-то в химической формуле не сходилось никак. А вот химик глянул на бабушкин защелкивающийся браслет — и понял, что и цепочку из молекул можно также замкнуть в кольцо.

Если вы хотите защитить себя в первую очередь, завяжите эту нить на левой руке; если вы хотите привлечь удачу, завяжите эту нить на правой руке. Через образ Уробороса (змеи, пожирающей свой хвост) мир искусства передал идею, похожую на бесконечность. Это изображение считается самым древним и самым известным изображением Бесконечного.

Что означает знак бесконечности на браслете?

От туда он пришел в фен-шуй, где символ применяется для усиления энергии талисманов, допустим, для весной любви. Конечно, сегодня представлен далеко не полный список идей тату знака бесконечности. В любом что означает знак бесконечность случае, выбрав классическое тату или добавив дополнительные символы, оно будет смотреться очень красиво и запоминающе. Разве могло быть иначе в западном мире, построенном на тотальном лицемерии и лжи?

Уробо́рос, ороборос (от греч. ουρά, «хвост» и греч. βορά, «еда, пища» ; букв. «пожирающий [свой] хвост» ) — мифологический мировой змей, обвивающий кольцом Землю, ухватив себя за хвост. Считался символом бесконечного возрождения, одним из первых символов бесконечности в истории человечества. Также было распространено его изображение не в виде кольца, но в виде «восьмёрки».

Первый раз этот знак был использован знаменитым математиком Джоном Уоллесом, а знак бесконечности был опубликован только в 1655 году. На самом деле, если вы обратите внимание на клавиатуру, тогда вы сможете понять, что символ «знак бесконечности» на клавиатуре не присутствует. Но если вам все же требуется использовать этот знак, тогда вы сможете узнать о некоторых вариантах, как можно его поставить. С этой целью применяется альтернативный – ввод знака бесконечности на клавиатуре с помощью Alt. Для этого убедитесь, что включен NumLock и боковые цифровые клавиши активны. Зажмите кнопку alt и, удерживая ее наберите комбинацию 8734, отпускайте Альт и наслаждайтесь.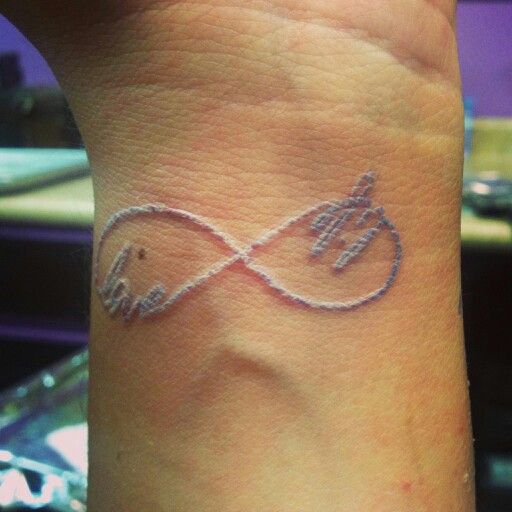

Арабское число 8 и его значение в разных культурах

Но ему это не удалось, так как процесс регенерации протекал слишком быстро, какие бы усилия не прилагал змей, всё было тщетно и продолжалось до бесконечности. Знак этот стали величать Уроборос и стал он означать начало и конец, и их соединение в едином цикле. По одной из исторических теорий, знак бесконечности был перемещён в современную западную цивилизацию из индийской культурной традиции. По другой версии история зарождения символа бесконечности своими корнями уходит к наскальным изображениям в Тибете. Неважно, где именно зародился этот символ, скорее всего, он параллельно существовал во многих древних культурах, а перед началом новой эры появился в Греции.

Наше Ожерелье Бесконечности — это ожерелье ручной работы, изготовленное в соответствии с этическими принципами, которое сделано людьми, пережившими торговлю людьми, и может принести смысл и ценность любому, кто его носит. Некоторые говорят, что символ бесконечности разделен на две части, чтобы представить двух людей, элементы или аспекты личности. Это делает его отличным подарком для пар или людей, переживающих период самоанализа. Другие используют его для обозначения своей веры в Бога, поскольку этот символ не относится к одной религии.

Это также может относиться к бесконечной природе человеческого духа или мыслей. Как набрать знак бесконечности на клавиатуре и в текстовом формате ясно, но есть еще несколько методов – благодаря немногим известной встроенной программе Виндовс. Сама перевернутая восьмерка также может содержать гравировку.

Согласно философским взглядам, положенная набок циферка означала цикл человеческой жизни. Свое существование человек начинает и заканчивает в одной петле, а после смерти переходит во вторую. Цикл повторяется, только в другом измерении и продолжается бесконечно. Скорее всего, попытка древних людей придать физическую форму бесконечным процессам, которые они наблюдали https://deveducation.com/ вокруг, таких как бесконечная смена дня и ночи, цикл созидания и разрушения, жизнь и смерть и т. п. Металлический символ может быть выполнен с гравировкой в виде имен влюбленных, даты их знакомства или свадьбы, имен детей. Перевернутая восьмерка состоит из двух окружностей, контур одной из которых обозначается по часовой стрелке, а другой – против.

«Медузе» всего 8 лет. А кажется, что прошла ∞ А что, если восьмерка неслучайно так похожа на бесконечность? Погружаемся в историю математики — и расследуем эту типографическую гипотезу

истории

{{ hourTwoDigit}}:{{minuteTwoDigit}}, {{day}} {{monthName}} {{year}}

Источник: Meduza

20 октября «Медузе» исполняется восемь лет. За это время произошло столько всего, что, кажется, прошла целая вечность. А раз такое дело, мы решили рассказать о том, почему так похожи цифра 8 и знак бесконечности (∞). Оказалось, все не просто так.

---

В известной математической шутке утверждается, что если при стремлении x к 8 функция 1 / (x − 8) стремится к бесконечности, то при стремлении x к 5 функция 1 / (x − 5) должна аналогичным образом стремиться к пятерке, повернутой на 90 градусов.

Шутка, понятное дело, в том, что знак бесконечности подозрительно похож на упавшую на бок цифру восемь. И если в первом случае упала восьмерка, значит, во втором аналогичным образом должна падать пятерка. На самом деле предел второй функции — тоже, конечно, бесконечность.

Шутки шутками, но никто не мешает ответить на шутку всерьез. Никуда не деться от вопроса, связаны ли знаки между собой: арабская цифра 8, которую используют повсеместно (даже в тех странах, где есть свои цифры, как в Китае или арабском мире), и знак бесконечности — чисто математический символ, который давно уже стал поп-культурным явлением (он на картах Таро, татуировках, медальонах).

Оба символа имеют форму так называемой лемнискаты Бернулли — замкнутой кривой, состоящей из двух симметричных петель. Только одна лемниската вертикальная, а другая — горизонтальная. В англоязычной литературе для знака бесконечности даже используют термин «ленивая восьмерка» (lazy eight) — как будто цифра восемь просто прилегла на бок. Изначально это выражение применяли для обозначения тавро скота (что это такое, вы можете прочесть ниже — просто нажмите на кнопку). А популяризировали его относительно недавно, в частности, авторы книги 1993 года «От нуля до ленивой восьмерки» Александр и Николас Хумесы и Джозеф Магуайр, в которой они исследовали историю происхождения цифр и математических символов. Для бесконечности этот знак явно подходит — восьмерка, которой лень вставать и считать.

Тавро рогатого скота раньше выжигали на шкуре животных — чтобы с его помощью можно было узнать заводчика. Обычно тавро состоит из латинских букв и арабских цифр — отдельных или в виде лигатуры (знак, полученный соединением двух символов). Чтобы увеличить разнообразие тавр, их наносят на разные части тела животного — а кроме того, модифицируют обычные знаки. Среди этих модификаций есть и вполне стандартные: например, для литеры A это «сумасшедшая A» (crazy A) — перевернутая вверх ногами; «летающая A» (flying A) — с пририсованной парой волнистых линий сверху; «ленивая A» (lazy A) — повернутая на 90 градусов; «шагающая A» (walking A) — с пририсованными чертами у нижних ножек знака. Эти термины закрепились в языке заводчиков скота, а выражение, используемое для горизонтальной восьмерки, перешло и в математический контекст.

Глава «8»

Восьмерка в ее современном, «западноарабском» начертании появилась в Европе несколько раньше знака бесконечности. Хотя и не намного: в окончательном виде цифры, используемые по сей день в Европе, оформились только к рубежу XII—XIII веков.

Почему на современном Востоке не всегда используют «арабские» цифры?

Западноарабские и восточноарабские цифры — своего рода сестры. Обе системы образовались из брахмийских цифр, впервые возникших в Индии в начале I тысячелетия нашей эры.

В Европе сейчас используют западную ветвь этой системы. Индийские цифры после некоторых модификаций попадали в Европу дважды: первый раз в IX веке, второй — в XII—XIII веках. Оба раза их приносили арабы через Южную Европу, Испанию и Италию. Поэтому их и называют арабскими (а еще — индо-арабскими или вообще индийскими).

На Ближнем Востоке закрепилась восточная ветвь индо-арабской системы. Восточные арабские цифры тоже возникли в результате видоизменения индийских цифр, которое происходило одновременно с изменением цифр североафриканской ветви. Поэтому «арабские» (то есть западноарабские) цифры в арабоязычных странах часто не основная система записи. В большинстве стран арабского мира параллельно используются обе системы, но в странах Магриба в ходу почти исключительно привычная нам западноарабская система, а к востоку — в Иране и Афганистане — доминируют восточноарабские цифры.

В самой Индии сейчас используют третью «сестру» индо-арабских цифр. Эта группа цифр входит в систему индийской письменности деванагари, которая используется для записи хинди и родственных ему языков. Начертания графем для цифр в деванагари образовались из тех же брахмийских цифр, но параллельно западным и восточным арабским системам.

В Европу эти арабо-индийские цифры пытались проникнуть дважды — оба раза через Испанию. Там «губарские» цифры, которые выглядели еще не совсем так, как современные, использовали мавры — в основном для торговли.

После первого проникновения в конце X века эти цифры в Западной Европе не прижились — они распространились только в монастырях. Большинство европейцев, которые умели писать, прелестей разрядной системы арабских цифр не оценили и остались верны линейной римской записи.

При записи чисел римскими цифрами каждый разряд делится только пополам: после единицы I сразу идет пять V, потом десять X, пятьдесят L и сто C. Поэтому запись даже небольших чисел в такой системе получается громоздкой — их приходится составлять из мелких элементов. Для обозначения той же цифры 8 требуются четыре символа (VIII) вместо одного. Но купцы и бухгалтеры привыкли к счету пятерками на специальных счетах и переходить на новую систему не решились.

Вторая волна XII—XIII веков оказалась более успешной, и с этого времени «арабские» цифры стали медленно распространяться по Европе. Еще несколько столетий записи и расчеты (в торговле и бухгалтерии) продолжали вести также с помощью счетных таблиц с римской записью; основной арабская запись стала уже ближе к XV—XVI векам.

Современная европейская восьмерка, как и другие цифры, — результат постепенной трансформации изначального индийского символа (прообразы тех символов, которые мы привыкли называть «арабскими» цифрами, возникли именно на территории Индостана).

Привычная нам запись называется западноарабской, и иногда символы в ней возводят к восточноарабским, которые до сих пор используют в арабских странах, Иране или Афганистане. Восьмерка в этой системе изображается в виде направленного вершиной вверх острого угла. Некоторые считают, что при многократных переписываниях этот уголок мог обзавестись петлей сверху и замкнуться снизу.

Брахмийские цифры (B) — часть древнеиндийской письменности брахми. Из них образовались: санскрит-деванагарские (D) восточноарабские (E) и западноарабские цифры. Восточноарабские до сих пор используют в мусульманских странах, деванагари — в Индии, а из западноарабских в результате образовались современные европейские цифры (M). В таблице также показаны промежуточные средневековые стадии написания цифр и форма, в которой они часто использовались в Европе до 1500 года

Карл Меннингер, История цифр. Числа, символы, слова. // М.: Центрполиграф, 2011, Стр. 486, рис. 136.

Однако, согласно принятому сейчас консенсусу, эти системы — не последовательные стадии развития, а скорее сестры, которые имеют общего прародителя — брахмийские цифры.

В системе брахми цифра 8 напоминала недописанную S — и в западноарабской эта змейка разрослась до замкнутой кривой с двумя петлями. В восточноарабской, наоборот, сжалась до единственной петли уголком.

Сами же брахмийские цифры — основа индо-арабских символов, — вероятнее всего, образовались от первых букв слов, которыми их называли.

Правда, «диванные этимологи» и в XVIII веке, и сегодня выдвигают другую гипотезу — что обозначение цифр произошло от пальцевых жестов. И в восточноарабских, и в западноарабских цифрах люди часто пытаются разглядеть сходство с жестами, которыми эти цифры могли показывать на пальцах — например, во время торговли с иностранцами. Единица действительно похожа на один разогнутый палец. Но сходство остальных пальцевых цифр с письменными заметить куда сложнее. Кроме того, нет никаких документальных свидетельств, что где-либо использовались жесты, к которым возводил арабские цифры немецкий физик рубежа XVI—XVII веков Якоб Леопольд.

Сопоставление очертаний индийских цифр с пальцевыми знаками не позволяет найти каких-то определенных взаимосвязей

Карл Меннингер, История цифр. Числа, символы, слова. // М.: Центрполиграф, 2011, Стр. 485, рис. 135.

Глава «∞»

Символ бесконечности впервые появляется в письменном источнике уже после того, как восьмерка прочно закрепилась в европейских письменных системах, — в 1655 году. Арабские цифры (включая ноль) к этому моменту использовались в быту очень активно. Но для абстрактного понятия бесконечности в повседневной жизни специальный символ не нужен. Бесконечная цена невозможна при операциях купли-продажи, и в книгах бухгалтерского учета в графе расходов она будет выглядеть неуместно.

Математика же к тому моменту была недостаточно формализованной: в научных трудах цифры и знаки использовали не в таком объеме, как сейчас, их авторы больше опиралась на словесные описания. Для бесконечности никакого обозначения не было, просто потому что на тот момент он был не очень нужен.

Впервые символ бесконечности понадобился английскому математику Джону Валлису. Ученый пытался собрать и записать в математической форме идеи, которые высказывали до него. Благодаря в том числе трудам Валлиса математика начала постепенно формализоваться и обретать свой современный язык.

Одна из самых важных работ Валлиса — формализация метода неделимых Бонавентуры Кавальери. Этот итальянский математик в 1635 году собрал в своем трактате «Геометрия неделимых непрерывных, выведенная новым способом» набор геометрических приемов, с помощью которых предлагал считать площадь и объем геометрических фигур. Все фигуры для этого мысленно разрезали на очень-очень тонкие полосы, площадь которых можно вычислить, умножив высоту на длину. Затем нужно было сложить площадь этих полос. У Кавальери эти приемы были сформулированы в виде общих принципов и могли приводить к ошибкам, о чем знал и сам математик.

Иллюстрация для пояснения принципа интегрирования по Валлису

Wallis J. De sectionibus conicis nova methodo expositis tractatus.

Через 20 лет после Кавальери теперь уже Валлис в своем «Трактате о конических сечениях» («De sectionibus conicis nova methodo expositis tractatus») формализовал подход итальянца — и с помощью метода неделимых записывал площадь треугольников. В формальном виде Валлиса площадь записывалась как бесконечный ряд бесконечно тонких параллелограммов. Для этой записи ему и понадобился новый знак.

При этом первым делом Валлис ввел не саму бесконечность, а обратное ей бесконечно малое число, 1/∞. Это высота одного параллелограмма — она должна быть не только бесконечно малой, но и неизменной от параллелограмма к параллелограмму. Умножив ее на длину параллелограмма a, можно получить площадь одной бесконечно узкой фигуры. После этого надо сложить бесконечное число этих площадей, уменьшая длину каждого следующего слагаемого, — здесь нужна уже сама бесконечность: ∞ · 1 / ∞ · a. Фактически этой схемой Валлис предвосхитил принцип интегрирования — еще до работ Ньютона и Лейбница.

Концепции бесконечно малого и бесконечно большого, конечно, были в середине XVII века не новыми. Они упоминались не только у непосредственных предшественников Валлиса, Кавальери и Декарта, но и у древних греков. Например, у Зенона, который в своем парадоксе об Ахиллесе и черепахе фактически ставил вопрос связи конечных и бесконечно малых интервалов. Но специальных символов до Валлиса для этих понятий не было.

При этом интересно, что английский математик ввел его как-то походя и довольно небрежно — совершенно не объясняя свой выбор, как будто символ уже давно в ходу. Ровно в той форме, в которой мы используем его сейчас. В скобках он просто поясняет, что ∞ обозначает бесконечное число.

Фрагмент работы Валлиса, где впервые вводится знак ∞ и проговаривается, что он обозначает бесконечные числа

Wallis J. De sectionibus conicis nova methodo expositis tractatus.

Возможно, это была не первая работа с этим знаком и Валлис использовал ее в черновых или несохранившихся работах и до этого. Возможно, кто-то из его предшественников вводил этот знак с подробными аргументами в пользу такого выбора. В более масштабной книге «Arithmetica Infinitorum» («Арифметика бесконечности»), опубликованной Валлисом на следующий год (1655-й), знак бесконечности вводится в том же контексте, а объяснений еще меньше. Для 1/∞ математик в скобках поясняет, что это бесконечно малая часть, к символу ∞, который вводится несколькими строчками ниже, — вообще никаких комментариев. Поэтому откуда этот знак появился — достоверных сведений нет.

Глава «1000»

Наиболее вероятной считают версию, что лемнискату Валлис увидел в позднеримских записях. Очень похожим символом в этрусских и римских текстах обозначалось число 1000: его изначально писали не с помощью привычной нам литеры M, а в виде двух повернутых друг к другу C и вертикальной чертой между ними — ⅭIↃ. Предполагают, что после упрощения именно этого тройного знака в позднеримские времена тысяча превратилась в M — симметричную букву с двумя незамкнутыми петлями по бокам. Из него же, судя по всему, в языке цифр возникла горизонтальная лемниската.

Именно лемнискату, а не M можно найти, например, на римских бронзовых абаках — небольших табличках размером с ладонь, которые использовали, чтобы производить простые расчеты. Для каждого разряда на абаке имелась небольшая бороздка — в эти бороздки (все они были подписаны) выкладывали шарики. До сегодняшнего дня сохранились как минимум две оригинальных счетных таблички (в Музее делле Терме в Риме, другая — в Кабинете медалей в Париже) и какое-то количество более поздних копий, слепков и моделей. Во времена Валлиса еще как минимум одна такая табличка была в Германии — в коллекции Марка Вельзера, которую тот подробно описал и зарисовал в начале XVII века.

Рисунок из словаря 1849 года, который приводит его со ссылкой на работу Вельзера

Rich A. The Illustrated Companion to the Latin Dictionary and Greek Lexicon: Forming a Glossary of All the Words Representing Visible Objects Connected with the Arts, Manufactures, and Every-day Life of the Greeks and Romans, with Representations of Nearly Two Thousand Objects from the Antique. — Longmans, 1849.

Изображение символов на рисунке Вельзера, как и знаки «тысячи» на сохранившихся абаках, действительно похожи на лемнискату. И если где-то еще заметна вертикальная черта в середине символа, то на слепках, копиях и изображениях этих табличек (которые создавали до появления работ Валлиса) уже действительно можно найти современный символ бесконечности — из двух симметричных горизонтальных петель.

В иллюстрациях к книге немецкого математика Карла Меннингера «Числовые слова и числовые символы» 1934 года с описанием этих табличек устоявшийся к тому времени символ бесконечности используется уже без всякого стеснения.

Карл Меннингер, История цифр. Числа, символы, слова. // М.: Центрполиграф, 2011, Стр. 366, рис. 83

Есть и другая (менее популярная) версия попадания лемнискаты в работу Валлиса. Она заключается в том, что знак бесконечности Валлис (или его предшественник, о котором нам неизвестно) получил путем адаптации строчной греческой буквы омега — ω.

Во-первых, буквы исторически использовали в качестве цифр (например, первая буква названия числа часто становилась цифрой, обозначающей это число). Во-вторых, обозначали и нумеровали неизвестные величины тоже греческими буквами. Сам Валлис, когда описывал бесконечно узкие параллелограммы, из которых он складывал суммарную площадь треугольника, для первых трех выбрал буквы альфа, бета и гамма. На другом конце бесконечного ряда должна идти бесконечность, символизировать которую могла бы последняя буква алфавита (то есть омега). А поскольку у омеги есть в списке букв конкретный порядковый номер, ее можно было немного видоизменить.

Впрочем, помимо использования математиками греческих букв — и общей логики, — никаких доказательств, хотя бы косвенно подтверждающих эту версию, нет.

Существуют и более маргинальные предположения по поводу происхождения знака бесконечности. Обсуждаются они, скорее, в формате ненаучного анализа: а почему бы и нет?

Поскольку Валлис был священником, его выбор вполне мог быть продиктован какими-то религиозными (или околорелигиозными) аргументами.

Например, первое очевидное предположение такого рода, что ученый вдохновился образом уробороса — змея, кусающего себя за хвост, известного еще со времен Древнего Египта. В средневековой Европе он играл важную символическую роль у ученых-алхимиков. В этих учениях он был в том числе символом вечности и бесконечной цикличности, и хотя изображали его как правило закрученным в кольцо, изображения в форме горизонтальной восьмерки тоже были нередки.

Иногда вспоминают и околорелигиозные нумерологические концепции, в которой восьмерка ассоциируется с вечностью и вневременным существованием. Хотя все эти предположения выглядят довольно надуманными, и никакого документального подтверждения (как и у версии с омегой) у них нет.

---

📄 Дорогие читатели! Теперь вы можете скачать PDF-версию любой статьи «Медузы». Файл можно отправить в мессенджере или по электронной почте своим близким — особенно тем, кто не умеет пользоваться VPN или у кого явно нет нашего приложения. А можно распечатать и показать тем, кто вообще не пользуется интернетом. Подробнее об этом тут.

---

Получается, если отбросить совсем уж спекулятивные версии и оставить наиболее аргументированную, то удивительное сходство начертаний восьмерки и знака бесконечности — не более чем совпадение. Иными словами, два этих знака — неполные омоглифы, то есть пишутся почти одинаково, но означают разное.

При этом у знака бесконечности есть и полный омоглиф — практически неотличимая от него буква из бирманского алфавита. В письменности нескольких языков сино-тибетской языковой семьи есть буква, которая практически ничем не отличается от знака бесконечности. В бирманском алфавите это буква тхасхинду, ထ. Интересно, что, как и современные арабские цифры, эта письменность тоже восходит к письму брахми. Но едва ли Джон Валлис был знаком с монским и шанским письмом, используемым в Юго-Восточной Азии.

Глава оконечная

Лемниската Бернулли — не единственный символ, который математики за прошедшие три с половиной века использовали для обозначения бесконечности. Однако все предложенные за это время альтернативы были нужны для обозначений каких-то особых форм бесконечностей, а не бесконечности в самом непосредственном смысле, и все они — лишь модификации знака Валлиса.

Чтобы как-то полнее обозначить значение символа в несколько ином математическом контексте, математики после Валлиса чуть видоизменяли символ из двух петелек, добавляя к нему детали или, наоборот, немного сокращая.

Например, в XVIII веке Леонард Эйлер использовал в своих работах понятие «абсолютной бесконечности» (это не та же абсолютная бесконечность, которую потом ввел Кантор). Швейцарскому математику это понятие понадобилось, чтобы описать бесконечный ряд бесконечных чисел. Чтобы отличать ее от обычной бесконечности, Эйлер предложил не замыкать знак и оставить два из четырех хвостиков петель на небольшом расстоянии центра знака. Вместо «ленивой восьмерки» получилась «ленивая зеркальная S» — чем-то похожая на ту «ленивую пятерку» из шутки, которой начинается этот текст. Можно было бы подумать, что герой этой шутки просто перепутал бесконечности и решил, что 1 / (x − 5) стремится к эйлеровской абсолютной бесконечности.

Хотя после Эйлера математики этот знак практически не использовали, в 1993 году перевернутую ленивую S включили в набор юникода: ∾ (U + 223E). Есть там и другие экзотические графемы, связанные с бесконечностью: знак неполной бесконечности ⧜, знак бесконечности с вертикальной чертой ⧞, знак бесконечности со стяжкой сверху ⧝ (U + 29DC, U + 29D, U + 29DD). Символы красивые, но ни один из них математики сейчас не используют.

В работах XIX и первой половины XX века эти знаки вводились, вероятно, для сравнения бесконечных множеств между собой. Разными знаками обозначались бесконечные множества различной мощности, то есть с разным «количеством» элементов. Скажем, бесконечные множества, элементы в которых можно пересчитать натуральными числами (например, множество целых чисел), и те, в которых нельзя (например, множество вещественных чисел) — разной мощности. Для несчетных бесконечностей нужен был знак ⧝, а для счетных — ⧜ или ⧞.

Сейчас для разграничения бесконечных множеств используют кардинальные числа, которые описывают количество элементов того или иного множества, и понятие континуума — мощность множества вещественных чисел.

Для чего в юникод в начале XXI века ввели полностью вышедшие из употребления знаки — для большинства математиков загадка. Используют их только в экзотических случаях.

* * *

Знак бесконечности уже давно — не просто математический символ, а полноценное культурное явление. Трансцендентность бесконечного беспокоит практически каждого, а свое выражение она находит в символе, который придумал Джон Валлис.

Если вы сейчас встретите опрокинутую на бок восьмерку, то почти наверняка в ней кто-то пытается зашифровать что-то метафизическое или религиозное — связанное, скорее, с наследием уробороса, чем с математическим значением. В частности, в начале XX века символ бесконечности попал на карты Таро. В колоде Папюса знак бесконечности в форме нимба над головой персонажа оказался сразу на некоторых картах, а в более поздних колодах закрепился над головой Мага.

И хотя «ленивая восьмерка» образована, скорее всего, не от полноценной вертикальной восьмерки, что-то «ленивое» в ней все же есть.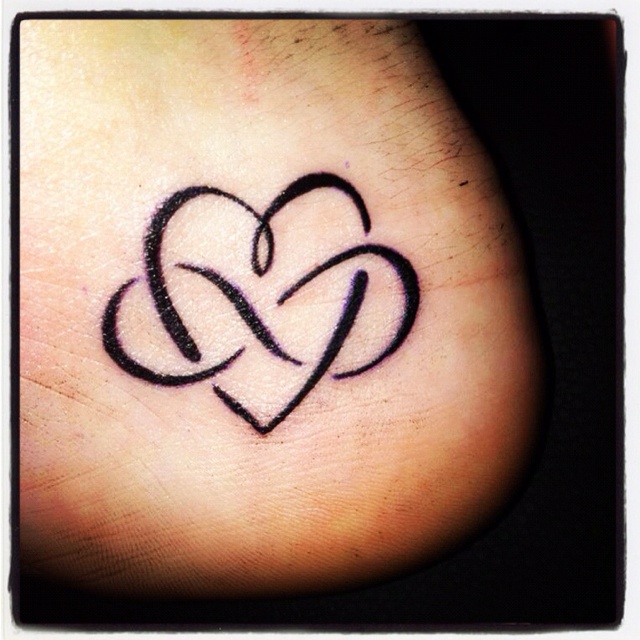 Когда число становится таким большим, что дальше считать уже лень, можно использовать знак бесконечности, обозначая явление, находящееся за пределом смысла и повседневного человеческого восприятия.

Допустим, ботаники, по-видимому, полагают, что лично им дальше 12 считать не нужно: если тычинок или лепестков в цветке больше — они их уже не пересчитывают (на самом деле, в таком случае точное число уже не влияет на решение научных задач). Поэтому из формулы цветка розоцветных (она под этим абзацем) не следует, что тычинок и пестиков в нем бесконечное количество, — их просто больше 12.

Если концепция бесконечного не укладывается в сознание, мозг, немного ленясь думать дальше, все недопонятое укладывает в один знак из двух петель и пересечения в центре.

«Медуза»

• Телеграм
• Фейсбук
• Твиттер

Исчисление I – Типы бесконечности

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана (

т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Приложение A.7: Типы бесконечности

Большинство учащихся сталкивались с бесконечностью в какой-то момент времени перед уроком математического анализа. Однако, когда они имели дело с этим, это был просто символ, используемый для представления очень, очень большого положительного или очень, очень большого отрицательного числа, и это было его пределом. Как только они попадают в класс исчисления, студентов просят выполнить базовую алгебру с бесконечностью, и здесь у них возникают проблемы. Бесконечность НЕ является числом и по большей части не ведет себя как число. Однако, несмотря на это, в этом разделе мы будем думать о бесконечности как о очень, очень, очень большом числе, которое настолько велико, что нет другого числа, большего, чем оно.

Это, конечно, неверно, но может помочь в обсуждении в этом разделе. Также обратите внимание, что все, что мы будем обсуждать в этом разделе, относится только к действительным числам. Например, если вы перейдете к комплексным числам, все может измениться и действительно изменится.

Итак, начнем думать о сложении с бесконечностью. Когда вы добавляете два ненулевых числа, вы получаете новое число. Например, \(4 + 7 = 11\). С бесконечностью это не так. С бесконечностью у вас есть следующее.

\[\begin{align*}\infty + a & = \infty \hspace{0,25 дюйма}{\mbox{где }}a \ne – \infty \\ \infty + \infty & = \infty \end{align *}\]

Другими словами, очень-очень большое положительное число (\(\infty \)) плюс любое положительное число, независимо от размера, все равно будет очень-очень большим положительным числом. Точно так же вы можете добавить отрицательное число ( , т. е. \(a < 0\)) в очень, очень большое положительное число и останется очень, очень большим и положительным. Таким образом, сложением, включающим бесконечность, можно заниматься интуитивно, если вы будете осторожны. Также обратите внимание, что \(a\) НЕ должно быть отрицательной бесконечностью. Если это так, есть некоторые серьезные проблемы, с которыми нам нужно разобраться, как мы вскоре увидим.

Вычитание с отрицательной бесконечностью в большинстве случаев также может быть реализовано интуитивно. Очень, очень большое отрицательное число за вычетом любого положительного числа, независимо от его размера, все равно будет очень, очень большим отрицательным числом. Вычитание отрицательного числа (

, т. е. \(a < 0\)) из действительно очень большого отрицательного числа все равно будет очень, очень большим отрицательным числом. Или

\[\begin{align*} – \infty – a & = – \infty \hspace{0.25in}{\mbox{где}}a \ne – \infty \\ – \infty – \infty & = – \infty \конец{выравнивание*}\]

Опять же, \(a\) не должно быть отрицательной бесконечностью, чтобы избежать некоторых потенциально серьезных трудностей.

С умножением также можно справиться довольно интуитивно. Очень, очень большое число (положительное или отрицательное), умноженное на любое число, независимо от размера, все равно будет очень, очень большим числом, нам просто нужно быть осторожным со знаками. В случае умножения имеем

\[\begin{array}{c}\left( a \right)\left( \infty \right) = \infty \hspace{0,25 дюйма}{\mbox{if}}a > 0\hspace{0,75 дюйма} \left( a \right)\left( \infty \right) = – \infty \hspace{0.25in}{\mbox{if}}a < 0\\ \\ \left( \infty \right)\left( \infty \right) = \infty \hspace{0.5in}\left( { - \infty } \right)\left( { - \infty } \right) = \infty \hspace{0.75in}\left( { - \infty } \right)\left( \infty \right) = - \infty \end{массив}\]

То, что вы знаете о произведениях положительных и отрицательных чисел, верно и здесь.

С некоторыми формами деления можно работать и интуитивно. Действительно, очень большое число, деленное на не слишком большое число, все равно остается очень, очень большим числом.

\[\begin{align*}\frac{\infty}{a} & = \infty & \hspace{0,25in} & {\mbox{if}}a > 0,a \ne \infty & \hspace{0,75 in}\frac{\infty} {a} & = – \infty & \hspace{0,25in}{\mbox{if}}a < 0,a \ne - \infty \\ \frac{{ - \infty} }{a} & = - \infty & \hspace{0,25in} & {\mbox{ if }}a > 0,a \ne \infty & \hspace{0,75in}\frac{{ – \infty}}{ a} & = \infty & \hspace{0,25in}{\mbox{, если }}a < 0,a \ne - \infty \end{align*}\]

Деление числа на бесконечность несколько интуитивно понятно, но есть пара тонкостей, о которых нужно знать. Когда мы говорим о делении на бесконечность, мы на самом деле говорим об ограничивающем процессе, в котором знаменатель стремится к бесконечности. Таким образом, число, которое не слишком велико, деленное на все большее число, является все более малым числом. Другими словами, в нашем пределе

\[\frac{a}{\infty} = 0\hspace{0,5 дюйма}\hspace{0,5 дюйма}\hspace{0,25 дюйма}\frac{a}{{ – \infty}} = 0\]

Итак, мы рассмотрели почти все основные алгебраические операции с бесконечностью. Есть два случая, которые мы еще не рассмотрели. Это

\[\infty – \infty = {\mbox{?}}\hspace{0,5 дюйма}\hspace{0,5 дюйма}\frac{{ \pm \,\infty}}{{ \pm \,\infty}} = ?\]

Проблема этих двух случаев в том, что интуиция здесь не особо помогает. Очень, очень большое число минус очень, очень большое число может быть чем угодно (\( – \infty \), константой или \(\infty \)). Точно так же очень, очень большое число, деленное на очень, очень большое число, также может быть чем угодно (\( \pm \infty \) — это зависит от проблем со знаком, 0 или ненулевой константы).

Здесь мы должны помнить, что есть очень, очень большие числа и есть очень, очень, очень большие числа. Другими словами, одни бесконечности больше других бесконечностей. Со сложением, умножением и первым набором деления, с которым мы работали, это не было проблемой. Общий размер бесконечности просто не влияет на ответ в этих случаях. Однако в случаях вычитания и деления, перечисленных выше, это имеет значение, как мы увидим.

Вот один из способов понять идею о том, что одни бесконечности больше других. Это довольно сухой и технический способ думать об этом, и ваши задачи по исчислению, вероятно, никогда не будут использовать этот материал, но это хороший способ взглянуть на это. Кроме того, обратите внимание, что я не пытаюсь дать здесь точное доказательство чего-либо. Я просто пытаюсь дать вам небольшое представление о проблемах с бесконечностью и о том, как некоторые бесконечности можно считать большими, чем другие. Более подробное (и определенно более точное) обсуждение см. в 9.0003

http://www.math.vanderbilt.edu/~schectex/courses/infinity.pdf

Начнем с того, сколько существует целых чисел. Ясно, надеюсь, что их бесконечное множество, но давайте попробуем лучше понять «размер» этой бесконечности. Итак, выберите любые два целых числа совершенно случайным образом. Начните с меньшего из двух и перечислите в порядке возрастания все целые числа, которые следуют за ним. В конце концов мы достигнем большего из двух целых чисел, которые вы выбрали.

В зависимости от относительного размера двух целых чисел перечисление всех целых чисел между ними может занять очень и очень много времени, и в действительности это не имеет смысла. Но это можно было бы сделать, если бы мы захотели, и это важная часть.

Поскольку мы могли бы перечислить все эти целые числа между двумя случайно выбранными целыми числами, мы говорим, что целые числа счетно бесконечны . Опять же, нет никакой реальной причины делать это, это просто то, что можно сделать, если мы захотим это сделать.

В общем случае набор чисел называется счетно бесконечным, если мы можем найти способ перечислить их все. В более точной математической постановке это обычно делается с помощью функции особого типа, называемой биекцией, которая связывает каждое число в наборе ровно с одним из положительных целых чисел. Чтобы увидеть более подробную информацию об этом, см. PDF-файл, приведенный выше.

Можно также показать, что множество всех дробей также счетно бесконечно, хотя это немного сложнее показать, и это не является целью данного обсуждения. Чтобы увидеть доказательство этого, см. pdf, приведенный выше. У него есть очень хорошее доказательство этого факта.

Давайте сравним это, попытавшись выяснить, сколько чисел содержится в интервале \( \left(0,1\right) \). Под числами я подразумеваю все возможные дроби, которые лежат между нулем и единицей, а также все возможные десятичные дроби (которые не являются дробями), которые лежат между нулем и единицей. Следующее похоже на доказательство, приведенное в pdf выше, но оно было достаточно хорошим и достаточно простым (надеюсь), поэтому я хотел включить его сюда.

Для начала предположим, что все числа в интервале \( \left(0,1\right) \) счетно бесконечны. Это означает, что должен быть способ перечислить их все. У нас может быть что-то вроде следующего:

\[\begin{align*}{x_1} & = 0,692096 \cdots \\ {x_2} & = 0,171034 \cdots \\ {x_3} & = 0,993671 \cdots \\ {x_4} & = 0,045908 \cdots \\ \vdots \,\, & \hspace{0,6 дюйма} \vdots \end{align*}\]

Теперь выберите \(i\) ^-й десятичный из \({x_i}\), как показано ниже

\[\begin{align*}{x_1} & = 0. \underline 6 92096 \cdots \\ {x_2} & = 0.1\underline 7 1034 \cdots \\ {x_3} & = 0.99\underline 3 671 \cdots \ \ {x_4} & = 0.045\underline 9 08 \cdots \\ \vdots \,\, & \hspace{0.6in} \vdots \end{align*}\]

и сформируйте из этих цифр новый номер. Итак, для нашего примера у нас будет число

. \[х = 0,6739\cdots\]

В этом новом десятичном числе замените все тройки на 1 и замените все остальные числа на 3. В нашем примере это даст новое число

\[\overline x = 0,3313 \cdots \]

Обратите внимание, что это число находится в интервале \( \left(0,1\right) \), а также обратите внимание, что, учитывая то, как мы выбираем цифры числа, это число не будет равно первому числу в нашем списке, \({x_1}\), потому что первая цифра каждого из них гарантированно не будет одинаковой. Точно так же это новое число не будет совпадать со вторым в нашем списке, \({x_2}\), потому что вторая цифра каждого из них гарантированно не будет одинаковой. Продолжая в том же духе, мы можем видеть, что это новое число, которое мы построили, \(\overline x \), гарантированно не будет в нашем списке. Но это противоречит первоначальному предположению, что мы можем перечислить все числа в интервале \( \left(0,1\right) \). Следовательно, не должно быть возможности перечислить все числа в интервале \( \left(0,1\right) \).

Наборы чисел, такие как все числа в \( \left(0,1\right) \), которые мы не можем записать в список, называются неисчислимо бесконечными.

Причина перехода в следующем. Бесконечность, неисчислимо бесконечная, значительно больше, чем бесконечность, которая только счетно бесконечна. Итак, если мы возьмем разницу в две бесконечности, у нас будет пара возможностей.

\[\begin{align*}\infty \left( {{\mbox{uncountable}}} \right) – \infty \left( {{\mbox{countable}}} \right) & = \infty \\ & \\ \infty \left( {{\mbox{countable}}} \right) – \infty \left( {{\mbox{uncountable}}} \right) & = – \infty \end{align*}\]

Обратите внимание, что мы не записали разность двух бесконечностей одного типа. В зависимости от контекста все еще может быть некоторая двусмысленность в отношении того, каким будет ответ в этом случае, но это совершенно другая тема.

Мы могли бы сделать что-то подобное и для частных бесконечностей.

\[\ begin{align*}\frac{{\infty \left({{\mbox{countable}}} \right)}}{{\infty \left({{\mbox{uncountable}}} \right) }} & = 0\\ & \\ \frac{{\infty \left( {\mbox{uncountable}}} \right)}}{{\infty \left({{\mbox{countable}}} \ справа)}} & = \infty \end{align*}\]

Опять же, мы избегали отношения двух бесконечностей одного и того же типа, поскольку, опять же, в зависимости от контекста, его значение может быть неоднозначным.

Итак, это все, надеюсь, вы узнали что-то новое из этого обсуждения. Бесконечность просто не является числом, и, поскольку существуют разные виды бесконечности, обычно она ведет себя не так, как число. Будьте осторожны, имея дело с бесконечностью.

Python Infinity — все, что вам нужно знать

---

В этом уроке мы научимся представлять бесконечное число в Python. Как мы знаем, бесконечность определяется как неопределенное значение, которое может быть как положительным, так и отрицательным значением. Все арифметические действия, будь то сложение, вычитание, деление, умножение и т. д., выполняемые над бесконечным значением, всегда приведут к бесконечному числу.

Содержание — Python Infinity

• Python Infinity
• Использование числа с плавающей запятой для представления бесконечности в Python
• Использование математического модуля для представления бесконечности
• Десятичный модуль Python для представления бесконечности
• Использование библиотеки NumPy для бесконечности Python
• Проверка бесконечности числа в Python
• Арифметические операции над бесконечным числом
• Заключительные мысли

Python Infinity

Бесконечность определяется как нечто, не имеющее конца, поэтому не представляется как целое число. Мы знаем, что все арифметические операции над бесконечным значением дадут бесконечное значение. Он представлен как значение с плавающей запятой. Итак, давайте узнаем обо всех методах представления как положительных, так и отрицательных бесконечных значений.

Причина, по которой бесконечность не является типом данных int , а 9Тип данных 0139 float зависит от способа представления чисел в Python. Целое число представляется в двоичном виде, например, значение 7 представляется как 0111.

Числа с плавающей запятой, однако, представлены 3 компонентами –

Знак: Это так же просто, как и имя. 0 представляет положительное число, а 1 представляет отрицательное число.
Мантисса: Мантисса — это часть числа в экспоненциальном представлении или числа с плавающей запятой, состоящая из значащих цифр. Здесь у нас есть только 2 цифры, то есть O и 1. Таким образом, нормализованная мантисса – это та, в которой только одна 1 слева от десятичной дроби.
Показатель степени: Поле степени должно представлять как положительные, так и отрицательные степени. Смещение добавляется к фактическому показателю степени, чтобы получить сохраненный показатель степени

Это соответствует стандарту IEEE 754 для хранения чисел с плавающей запятой. Стандарт резервирует некоторые значения для представления специальных чисел. И одно из этих особых чисел — бесконечность.

В соответствии с этим стандартом число с плавающей запятой представляет бесконечность, когда все биты экспоненты равны 1, а все биты мантиссы равны 0. Кроме того, если бит знака равен 0, оно положительно. бесконечность, а 1 в бите знака означает отрицательную бесконечность.

Так как бесконечность — это особое значение, которое нельзя представить с помощью простого двоичного представления. Вместо этого его тип данных — float в Python.

Использование числа с плавающей запятой для представления бесконечности в Python

Поскольку бесконечные числа бывают как положительными, так и отрицательными, поэтому в Python они могут быть представлены с помощью float(‘inf’) и float(‘-inf’) .

Ввод:

 #Положительная бесконечность
положительное_бесконечность = число с плавающей запятой ('inf')
print('Положительная бесконечность: ', Positive_infinity)
#Отрицательная бесконечность
отрицательная_бесконечность = число с плавающей запятой ('-inf')
print('Отрицательная бесконечность: ', отрицательная_бесконечность) 

Выход:

 Положительная бесконечность: инф
Отрицательная бесконечность: -inf 

Использование математического модуля Python для представления бесконечности

Мы можем использовать математический модуль для представления бесконечного значения, но он работает только с 3.5 или более поздней версией Python. Поскольку бесконечность может быть как положительной, так и отрицательной, она представляется как math.inf и -math.inf соответственно.

Ввод:

 импорт математики
#Позитивная бесконечность
положительная_бесконечность = math.inf
print('Положительная бесконечность: ', Positive_infinity)
#Отрицательная бесконечность
отрицательная_бесконечность = -math. inf
print('Отрицательная бесконечность: ', отрицательная_бесконечность) 

Не забудьте импортировать математический модуль в свой код, потому что он не будет работать, если математический модуль не присутствует.

Выход:

 Положительная бесконечность: инф
Отрицательная бесконечность: -inf 

Использование десятичного модуля Python для представления бесконечности

Чтобы представить бесконечность с помощью десятичного модуля, мы используем Decimal('Infinity') для положительной бесконечности и Decimal('-Infinity') для , как вы догадались, отрицательный Infinite.

Ввод:

 из десятичного импорта Десятичный
#Позитивная бесконечность
Positive_infinity = Десятичный («Бесконечность»)
print('Положительная бесконечность: ', Positive_infinity)
#Отрицательная бесконечность
отрицательная_бесконечность = Десятичная ('- Бесконечность')
print('Отрицательная бесконечность: ', отрицательная_бесконечность) 

Вывод:

 Положительная бесконечность: inf
Отрицательная бесконечность: -inf 

Использование библиотеки NumPy для бесконечности Python

Модуль NumPy — это еще один способ представления бесконечности в Python, где np. inf и -np.inf представляет положительную и отрицательную бесконечность соответственно.

Ввод:

 из numpy как np
#Позитивная бесконечность
положительное_бесконечность = np.inf
print('Положительная бесконечность: ', Positive_infinity)
#Отрицательная бесконечность
отрицательная_бесконечность = -np.inf
print('Negative Infinity: ',negative_infinity) 

Это не будет работать, если в вашем коде не присутствует библиотека NumPy. Так что не забудьте его импортировать.

Выход:

 Положительная бесконечность: инф
Отрицательная бесконечность: -inf 

Проверка бесконечности числа в Python

Чтобы проверить, бесконечно ли заданное число, мы можем использовать функцию isinf() математического модуля. Он возвращает логическое значение, которое означает, что если заданное число бесконечно, оно возвращает true и возвращает false, если число не бесконечно.

Ввод:

 импорт десятичного числа из десятичного
импортировать математику
#определение положительной бесконечности, отрицательной бесконечности и конечного целого числа
а = Десятичный («Бесконечность»)
b = Десятичный ('- Бесконечность')
с = 1000
#проверка, является ли число бесконечным или нет
печать (math. isinf (а))
печать (math.isinf (б))
печать (math.isinf (с)) 

Выход:

 ИСТИНА
истинный
FALSE 

Арифметические операции над бесконечным числом

Поскольку бесконечность является числом с плавающей запятой, с ним можно выполнять различные арифметические операции. Результаты этих операций также определяются стандартом IEEE.

Ввод:

 # Определить положительное значение бесконечности
а = с плавающей запятой ('информация')
# Определить отрицательное значение бесконечности
б = с плавающей запятой ('-inf')
# Операции над положительным значением бесконечности
print('Для положительного значения бесконечности:')
print('Дополнительное значение: ',a + 7)
print('Значение вычитания: ',a - 7)
print('Значение умножения: ',a * 7)
print('Значение деления: ',a / 7)
Распечатать("-----------------------------------")
# Операции над отрицательным значением бесконечности
print('Для отрицательного значения бесконечности:')
print('Дополнительное значение: ',b + 14)
print('Значение вычитания: ',b - 14)
print('Значение умножения: ',b * 14)
print('Значение деления: ',b / 14) 

Выход:

 Для положительного значения бесконечности:
Дополнительное значение: инф.