Значение ромба: Ромб

Содержание

Ромб — Википедия

Материал из Википедии — свободной энциклопедии

Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны^[1].

Этимология

Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.

Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.

Свойства

Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны, АВ || CD, AD || ВС.
Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре прямоугольных треугольника.
Диагонали ромба являются биссектрисами его углов (∠ DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
Середины четырех сторон ромба являются вершинами прямоугольника.
Диагонали ромба являются перпендикулярными осями его симметрии.
В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Признаки

Параллелограмм ABCD{\displaystyle ABCD} является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий^[2]:

Две его смежные стороны равны (отсюда следует, что все стороны равны, AB=BC=CD=AD{\displaystyle AB=BC=CD=AD}).
Его диагонали пересекаются под прямым углом (AC ⊥ BD).
Одна из диагоналей делит содержащие её углы пополам.

Предположим, что заранее не известно, что четырёхугольник является параллелограммом, но дано, что все его стороны равны. Тогда этот четырёхугольник есть ромб

[1].

Квадрат, как частный случай ромба

Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. {2}}}}}.}

В геральдике

Ромб является простой геральдической фигурой.

Червлёный ромб в серебряном поле
В червлёном поле 3 сквозных ромба: 2 и 1
Просверленный червлёный ромб в серебряном поле
В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов

Симметрия

Ромб симметричен относительно любой из своих диагоналей, поэтому часто используется в орнаментах и паркетах.

Ромбический орнамент
Ромбические звёзды
Более сложный орнамент
Орнамент из ромбов и квадратов

См. также

Литература

Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.

Примечания

↑ ¹ ² Элементарная математика, 1976, с. 435..
↑ Элементарная математика, 1976, с. 435—436..
↑ Ромб // Малый академический словарь. — М.: Институт русского языка Академии наук СССР. Евгеньева А. П.. 1957—1984.
↑ Ромб // Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910

↑ Ромб // Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней. Михельсон А.Д., 1865
↑ Weisstein, Eric W. Rhombus (англ.) на сайте Wolfram MathWorld.

Логотип Рено – как выглядит, история | Дизайн, лого и бизнес

Компания Рено (оригинальное название «Renault Group») — масштабная всемирно известная французская корпорация, основным видом деятельности которой является производство высокотехнологичного, качественного, безопасного транспорта. На сегодняшний день фирма является частью гигантского альянса «Renault–Nissan–Mitsubishi». Штаб-квартира компании расположена недалеко от Парижа, в городе Булонь-Бийанкуре.

Разработать логотип для бизнеса за 5 минут

Нажмите кнопку «Создать логотип» и конструктор бесплатно предложит для вас варианты лого. Просто выбирайте и начинайте работать!

Популярность бренда быстро увеличивалась благодаря внедрению в производство передовых технологий. Такой подход делал автомобили компании широко востребованными по всему миру. В настоящий момент корпорация Рено занимается производством авто с учетом климатических условий страны, в которой будет реализовываться продукция бренда.

История бренда Рено

В 1898 году три брата Рено (Луи, Марсель и Фернан) создают бренд «Société Renault Frères». К концу года предприятие демонстрирует первый разработанный автомобиль. Отличительная особенность произведенного авто — наличие первой в мире коробки передач с прямой высшей передачей.

1902 год — Луи Рено решает получить патент на свое изобретение — нагнетенный процессор (позже трубонаддув). А спустя два года патентует конструкцию съемной свечи зажигания. В 1917 году руководитель компании Луи Рено создаёт первый в мире танк классической компоновки (Рено FT).

В 1944 Луи Рено умирает, из-за чего компания переходит правительству Франции. Но на этом деятельность фирмы не заканчивается. Уже спустя 2 года Рено выпускает седан Renault 4CV. А к 1985 году бренд начинает выпускать первые в мире минивэны (Renault Espace).

1996 год — компанию приватизируют, в последствие чего ее название изменяется на «Renault S.A.».

Значение логотипа Рено

О том, что означает логотип Рено, задумываются тысячи автолюбителей. Выдвигаются самые разные предположения, но об истинном смысле, зашифрованном в фигуре, догадываются не все. Логотип машины Рено (ромб) — это схематичное изображение алмаза: именно так изначально задумывалось братьями-создателями.

Логотипы Рено разных годов

История логотипа Рено невероятно богата: она отражает все ключевые этапы развития бренда. Удобнее всего отслеживать изменения логотипов Рено по фото.

1899 год — первый логотип Рено представляет собой горизонтально вытянутый овал, украшенный сверху вензелями. Внутри него располагаются инициалы основателей бренда. Буквы выполнены оригинальным шрифтом, напоминающим рукописный. Внутренняя часть овала также дополнена окантовкой, похожей на мелкие бусы. Такой вариант дизайна логотипа использовался компанией 7 лет.

1906 год — эмблема становится круглой. Из фигуры исчезают инициалы. Внутри сферы, по периметру, находится многогранная шестерёнка. В центре композиции изображён спортивный автомобиль. Логотип, также как и в предыдущем варианте, представлен в черно-белой расцветке.

1919 год — логотип снова претерпевает значительные изменения, сохраняется только форма. Внутрь чёрного широкого круга в полупрофиль вставлено изображение танка, немного выходящего за пределы фигуры.

1923 год — фирменным знаком Рено становится радиаторная решётка, помещенная внутрь белой окружности. В середину решетки вставлена рубленая надпись «Renault».

1925 год — решётка трансформируется в ромб, олицетворяющий алмаз. Это дизайнерское решение положило начало современному логотипу Рено. В средней части ромба размещено слово «Renault», дополненное по краям двумя черными точками.

1946 год — теперь ромб становится более вытянут вертикально. Изменяется и расцветка логотипа: добавляется жёлтый цвет (в него окрашена внутренняя часть отсеков решетки). На эмблеме наряду с названием компании появляется надпись «Regie Nationale». Изменяется и шрифт текста: он становится более жирным, исчезают засечки.

1959 год — эмблема снова становится чёрно-белой. Форма ромба сохраняется, как и надпись посередине. Но буквы становятся более вытянутые.

1972 год — логотип Рено становится минималистичным. Теперь ромб пуст внутри, а его широкие грани дополнены параллельными полосами. Фон окрашивается в приглушенным желтый цвет. Надпись «Renault» смещается под ромб, буквы снова обретают засечки.

1992 год — эмблема избавляется от некоторых элементов: остается только стилизованный ромб (как и в прошлой версии лого). Также исчезает надпись, фон становится белым.

2004 год — вид ромба значительно изменяется, из него исчезают полосы. Две нижние части фигуры закрашены черным цветом, а верхние — остаются белыми. Ромб дополнен черной окантовкой. В данном варианте логотипа снова появляется наименование бренда, но теперь оно расположено внизу и имеет черное подчеркивание.

2007 год — слово «Renault» также находится под графической композицией. Ромб становится крупнее, его текстура напоминает серебряные слитки. Возвращается желтая заливка фона.

2015 год — принимается дизайн логотипа, который используется компанией в настоящее время. Теперь эмблема состоит только из изображения ромба, который был на логотипе 2007 года. Исчезла надпись, фон снова окрашен в белый.

Заключение

Логотип Рено выглядит стильно и презентабельно: он рассказывает интереснейшую историю одного из ведущих автопроизводителей Новейшего времени.

Другие статьи

Продуктовый и графический дизайнер с опытом работы более 10 лет. Пишу о брендинге, дизайне логотипов и бизнесе.

Ромб, свойства, признаки, формулы, площадь и периметр

Ромб, свойства, признаки, формулы, площадь и периметр.

Ромб – это параллелограмм, у которого все стороны равны.

Ромб (определение и понятие)

Видеоурок “Ромб”

Свойства ромба

Признаки ромба

Формулы ромба. Площадь ромба. Периметр ромба

Ромб (определение и понятие):

Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе – «бубен») – это параллелограмм, у которого все стороны равны.

Рис. 1. Ромб

Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма.

Ромбы отличаются друг от друга размером углов и длиной стороны.

Если у ромба – прямые углы, то он называется

квадратом.

@ https://youtu.be/AavypoP06_U

Свойства ромба:

1. Противолежащие стороны ромба равны, т. к. все стороны ромба равны.

Рис. 2. Ромб

AB = BC = CD = AD

2. Противолежащие стороны ромба попарно параллельны.

Рис. 3. Ромб

АВ || CD, AD || ВС

3. Соседние углы ромба дополняют друг друга до 180°. Иными словами, сумма углов, прилежащих к любой из сторон ромба, равна 180°.

Рис. 4. Ромб

∠CDA + ∠DAB = 180°

4. Диагонали ромба взаимно перпендикулярны.

Рис. 5. Ромб

AC ⊥ BD

5. Диагонали ромба точкой пересечения делятся пополам.

Рис. 6. Ромб

BO = OD, AO = OC

6. Диагонали ромба делят ромб на четыре прямоугольных треугольника.

Рис. 7. Ромб

7. Диагонали ромба являются биссектрисами его углов и делят углы пополам.

Рис. 8. Ромб

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

8. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре.

Рис. 9. Ромб

AC² + BD² = 4AB²

9. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Центром окружности вписанной в ромб будет точка пересечения его диагоналей.

Рис. 10. Ромб

Признаки ромба:

Параллелограмм ABCD является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий:

– если две смежные стороны параллелограмма равны (отсюда следует, что все стороны равны), то он является ромбом.

AB = BC, то AB = BC = CD = AD;

– если диагонали параллелограмма пересекаются под прямым углом, то он является ромбом.

AC ⊥ BD;

– если одна из диагоналей параллелограмма делит содержащие её углы пополам, то он является ромбом.

∠BAC = ∠CAD или ∠ABD = ∠DBC или ∠BCA = ∠ACD или ∠ADB = ∠BDC;

– если в параллелограмм можно вписать круг, то он является ромбом;

– если диагонали делят параллелограмм на четыре равных прямоугольных треугольника, то он является ромбом.

Квадрат

Прямой угол

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Ромб

Шестиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Видео https://youtu.be/AavypoP06_U

Найти что-нибудь еще?

Крест, Трезубец, Ромб и др

Одиноких девушек зачастую волнует вопрос замужества. Найти ответ можно на своей руке, если посмотреть на линии расположенные на холме Меркурия и на ребре ладони. Так можно определить количество бракосочетаний, любовных связей и увлечений.

Общее значение

Полоски на ребре — отображение близких людей, с которыми возникнет тесная взаимосвязь. Узнать количество крепких отношений и брачных союзов можно, если их посчитать.

Что означают другие символы:

Ярко выраженная полосочка без всяких фигур на конце предзнаменует стабильный союз.
Слабовыраженные отметки — это временные связи, которые не закончатся ничем серьёзным.
Отсутствие чёрточек — негативный показатель, свидетельствующий о том, что на человека наложено проклятие под названием «Венец безбрачия».
Отсутствие бороздочек также может быть в случае, если замужество было сделано по расчёту.

Ромб, квадрат, трапеция

Ромб, квадрат или трапеция в этом месте являются положительными символами и означают покровительство Высших сил. Данные фигуры защитят владельца от обмана, измены, а также помогут определить альфонса. Это символы счастливой долгой супружеской жизни полной любви и понимания.

Случается, что треугольник аккуратно переходит в ромб, это предвестник частных ссор и непонимания. Но человек с таким знаком не будет воспринимать всё близко к сердцу.

Человек с квадратом или ромбом на линии Брака трезво смотрит на происходящее, он не будет погружаться в любовь с головой и продумает все варианты, которые могут возникнуть в результате.

Если символ расположен в центре черты, то предзнаменует чистую и страстную любовь.
Черта Брака с ромбом в середине предостерегает, что избранный окажется эгоистом. Существует риск, что вторая половинка окажется в тюрьме. Подтверждает это крест внутри фигуры.

Если отметка располагается в конце линии Брака, это говорит о конфликтах, но побеждать в них всегда будет обладатель данного знака.

Прерывистые отрезки символизируют негатив, но если они попадают в квадрат, то он смягчает плохое.

Обладатели квадрата защищены небесами. Он представляет собой талисман, оберегающий от обмана, одиночества или безответных чувств.

Трезубец

Трезубец — неоднозначный знак. Если он имеется на Брачной борозде, то вскоре завяжутся серьёзные отношения, но радости они не принесут. Партнёры будут вести борьбу за лидерство, из-за этого могут пострадать дети либо искра любви погаснет навсегда.

Если есть трезубец на линии Брака, который проходит мимо дуги Сердца, это свидетельствует о том, что у человека будет одна любовь на всю жизнь.
Если полосочка Брака заканчивается трезубцем — проблемы, которые могут послужить причиной развода. Возможно, супругам стоит хорошо проанализировать происходящее, сделать выводы и пересмотреть взаимоотношения.
Пересечение бороздки с трезубцем, который идёт от холма Юпитера, свидетельствует о спутанных чувствах. У обладателя такого пересечения в личной жизни имеется связь на стороне.

Если символ примыкает со стороны холма Марса, это говорит о коротких любовных увлечениях. У человека нет желания создавать семью.

Крест

Фигура в виде креста пугает людей, особенно если она появляется на полоске Супружества. Преждевременно волноваться не стоит, поскольку хиромантия только предупреждает человека, но не утверждает что-либо, поэтому всегда можно изменить жизнь в лучшую сторону.

Значения:

На этой линии — признак ссор со второй половинкой, но это не означает, что наступит развод.
Мелкие чёрточки, пересекающие полосу говорят о частых скандалах, финансовых проблемах и других трудностях в семейной жизни.

Отличным признаком будет исчезновение такой фигуры, это говорит о том, что человек, много работал над собой, чтобы создать гармоничные отношения в семье. При появлении подобной отметки стоит задуматься о том, что вызывает раздор.

Крест в хиромантии имеет негативное значение, если он расположен вначале либо в середине, это говорит о проблемах возникающими между мужем и женой.

Если он образуется из полоски, отвечающей за потомство, и черты супружества, это означает, что супруги будут заботливыми родителями.

Треугольник

Появление треугольника на черте Супружества, к сожалению, не очень хороший предвестник. Он говорит, что в семейной жизни будут проблемы, между супругами и/или же ваши, что помешает счастью.

Внимание необходимо обратить на расположение знака:

В начале — редко встречается, и говорит о том, что в этих отношениях будет ждать недоверие, измены и другие неприятные события.
В середине — негативные события будут связаны с детьми.
В конце — более менее нейтральный вариант. Прожив всю жизнь с выбранным человеком, лишь в конце вы возможно разочаруетесь в нем.

Наиболее подробно о всех вариантах треугольника на ниточке Супружества можно прочесть в статье: https://arcany.ru/hiromantiya/treugolnik-na-linii-braka-v-konce-v-nachale-ravnostoronnij.html

Остров

Одним из неприятных символов, который можно встретить — остров.

Остров на супружеской дуге — проблемные отношения.

Варианты расположения:

В начале — относительно благоприятная интерпретация, связанная с тем, что непонимание будет только первое время.
В середине — возникновение разногласий, но если после острова линия продолжается, то пара придет к консенсусу.
На конце он предвещает очень скандальный развод, из которого супруги выйдут врагами на всю жизнь.

Звезда

Наиболее редко встречающий в этом месте символ, который

говорит о заключении союза по расчету.

Появляется у тех, кто принял решение подняться в социальном статусе таким способом. Характерно в случаях, где у партнеров очень большая разница в возрасте.

Расположение:

В начале — сложности в паре, которые могут быть связаны как с изменой одного из супругов, так и не пониманием родителей и детей.
В конце — чаще всего негативный знак, говорящий о разрыве, но это могут быть интрижки на стороне.

Заключение

С помощью знаков на линии Брака можно узнать прошлое и настоящее. Будущее зависит от действий человека, поэтому не стоит волноваться, лучше использовать всё силы для изменения ситуации в лучшую сторону.

К примеру, если предначертаны проблемы в бизнесе, это не вердикт, а предупреждение, что следует пересмотреть деловые связи, возможно, партнёр нечестен с вами.

Значение слова «ромб»

Лексическое значение: определение

Общий запас лексики (от греч. Lexikos) — это комплекс всех основных смысловых единиц одного языка. Лексическое значение слова раскрывает общепринятое представление о предмете, свойстве, действии, чувстве, абстрактном явлении, воздействии, событии и тому подобное. Иначе говоря, определяет, что обозначает данное понятие в массовом сознании. Как только неизвестное явление обретает ясность, конкретные признаки, либо возникает осознание объекта, люди присваивают ему название (звуко-буквенную оболочку), а точнее, лексическое значение. После этого оно попадает в словарь определений с трактовкой содержания.

Словари онлайн бесплатно — открывать для себя новое

Словечек и узкоспециализированных терминов в каждом языке так много, что знать все их интерпретации попросту нереально. В современном мире существует масса тематических справочников, энциклопедий, тезаурусов, глоссариев. Пробежимся по их разновидностям:

Толковые Найти значение слова вы сможете в толковом словаре русского языка. Каждая пояснительная «статья» толкователя трактует искомое понятие на родном языке, и рассматривает его употребление в контенте. (PS: Еще больше случаев словоупотребления, но без пояснений, вы прочитаете в Национальном корпусе русского языка. Это самая объемная база письменных и устных текстов родной речи.) Под авторством Даля В.И., Ожегова С.И., Ушакова Д.Н. выпущены наиболее известные в нашей стране тезаурусы с истолкованием семантики. Единственный их недостаток — издания старые, поэтому лексический состав не пополняется.
Энциклопедические В отличии от толковых, академические и энциклопедические онлайн-словари дают более полное, развернутое разъяснение смысла. Большие энциклопедические издания содержат информацию об исторических событиях, личностях, культурных аспектах, артефактах. Статьи энциклопедий повествуют о реалиях прошлого и расширяют кругозор. Они могут быть универсальными, либо тематичными, рассчитанными на конкретную аудиторию пользователей. К примеру, «Лексикон финансовых терминов», «Энциклопедия домоводства», «Философия. Энциклопедический глоссарий», «Энциклопедия моды и одежды», мультиязычная универсальная онлайн-энциклопедия «Википедия».
Отраслевые Эти глоссарии предназначены для специалистов конкретного профиля. Их цель объяснить профессиональные термины, толковое значение специфических понятий узкой сферы, отраслей науки, бизнеса, промышленности. Они издаются в формате словарика, терминологического справочника или научно-справочного пособия («Тезаурус по рекламе, маркетингу и PR», «Юридический справочник», «Терминология МЧС»).
Этимологические и заимствований Этимологический словарик — это лингвистическая энциклопедия. В нем вы прочитаете версии происхождения лексических значений, от чего образовалось слово (исконное, заимствованное), его морфемный состав, семасиология, время появления, исторические изменения, анализ. Лексикограф установит откуда лексика была заимствована, рассмотрит последующие семантические обогащения в группе родственных словоформ, а так же сферу функционирования. Даст варианты использования в разговоре. В качестве образца, этимологический и лексический разбор понятия «фамилия»: заимствованно из латинского (familia), где означало родовое гнездо, семью, домочадцев. С XVIII века используется в качестве второго личного имени (наследуемого). Входит в активный лексикон. Этимологический словарик также объясняет происхождение подтекста крылатых фраз, фразеологизмов. Давайте прокомментируем устойчивое выражение «подлинная правда». Оно трактуется как сущая правда, абсолютная истина. Не поверите, при этимологическом анализе выяснилось, эта идиома берет начало от способа средневековых пыток. Подсудимого били кнутом с завязанными на конце узлом, который назывался «линь». Под линью человек выдавал все начистоту, под-линную правду.
Глоссарии устаревшей лексики Чем отличаются архаизмы от историзмов? Какие-то предметы последовательно выпадают из обихода. А следом выходят из употребления лексические определения единиц. Словечки, которые описывают исчезнувшие из жизни явления и предметы, относят к историзмам. Примеры историзмов: камзол, мушкет, царь, хан, баклуши, политрук, приказчик, мошна, кокошник, халдей, волость и прочие. Узнать какое значение имеют слова, которые больше не употребляется в устной речи, вам удастся из сборников устаревших фраз. Архаизмамы — это словечки, которые сохранили суть, изменив терминологию: пиит — поэт, чело — лоб, целковый — рубль, заморский — иностранный, фортеция — крепость, земский — общегосударственный, цвибак — бисквитный коржик, печенье. Иначе говоря их заместили синонимы, более актуальные в современной действительности. В эту категорию попали старославянизмы — лексика из старославянского, близкая к русскому: град (старосл.) — город (рус.), чадо — дитя, врата — ворота, персты — пальцы, уста — губы, влачиться — волочить ноги. Архаизмы встречаются в обороте писателей, поэтов, в псевдоисторических и фэнтези фильмах.
Переводческие, иностранные Двуязычные словари для перевода текстов и слов с одного языка на другой. Англо-русский, испанский, немецкий, французский и прочие.
Фразеологический сборник Фразеологизмы — это лексически устойчивые обороты, с нечленимой структурой и определенным подтекстом. К ним относятся поговорки, пословицы, идиомы, крылатые выражения, афоризмы. Некоторые словосочетания перекочевали из легенд и мифов. Они придают литературному слогу художественную выразительность. Фразеологические обороты обычно употребляют в переносном смысле. Замена какого-либо компонента, перестановка или разрыв словосочетания приводят к речевой ошибке, нераспознанному подтексту фразы, искажению сути при переводе на другие языки. Найдите переносное значение подобных выражений в фразеологическом словарике. Примеры фразеологизмов: «На седьмом небе», «Комар носа не подточит», «Голубая кровь», «Адвокат Дьявола», «Сжечь мосты», «Секрет Полишинеля», «Как в воду глядел», «Пыль в глаза пускать», «Работать спустя рукава», «Дамоклов меч», «Дары данайцев», «Палка о двух концах», «Яблоко раздора», «Нагреть руки», «Сизифов труд», «Лезть на стенку», «Держать ухо востро», «Метать бисер перед свиньями», «С гулькин нос», «Стреляный воробей», «Авгиевы конюшни», «Калиф на час», «Ломать голову», «Души не чаять», «Ушами хлопать», «Ахиллесова пята», «Собаку съел», «Как с гуся вода», «Ухватиться за соломинку», «Строить воздушные замки», «Быть в тренде», «Жить как сыр в масле».
Определение неологизмов Языковые изменения стимулирует динамичная жизнь. Человечество стремятся к развитию, упрощению быта, инновациям, а это способствует появлению новых вещей, техники. Неологизмы — лексические выражения незнакомых предметов, новых реалий в жизни людей, появившихся понятий, явлений. К примеру, что означает «бариста» — это профессия кофевара; профессионала по приготовлению кофе, который разбирается в сортах кофейных зерен, умеет красиво оформить дымящиеся чашечки с напитком перед подачей клиенту. Каждое словцо когда-то было неологизмом, пока не стало общеупотребительным, и не вошло в активный словарный состав общелитературного языка. Многие из них исчезают, даже не попав в активное употребление. Неологизмы бывают словообразовательными, то есть абсолютно новообразованными (в том числе от англицизмов), и семантическими. К семантическим неологизмам относятся уже известные лексические понятия, наделенные свежим содержанием, например «пират» — не только морской корсар, но и нарушитель авторских прав, пользователь торрент-ресурсов. Вот лишь некоторые случаи словообразовательных неологизмов: лайфхак, мем, загуглить, флэшмоб, кастинг-директор, пре-продакшн, копирайтинг, френдить, пропиарить, манимейкер, скринить, фрилансинг, хедлайнер, блогер, дауншифтинг, фейковый, брендализм. Еще вариант, «копираст» — владелец контента или ярый сторонник интеллектуальных прав.
Прочие 177+ Кроме перечисленных, есть тезаурусы: лингвистические, по различным областям языкознания; диалектные; лингвострановедческие; грамматические; лингвистических терминов; эпонимов; расшифровки сокращений; лексикон туриста; сленга. Школьникам пригодятся лексические словарники с синонимами, антонимами, омонимами, паронимами и учебные: орфографический, по пунктуации, словообразовательный, морфемный. Орфоэпический справочник для постановки ударений и правильного литературного произношения (фонетика). В топонимических словарях-справочниках содержатся географические сведения по регионам и названия. В антропонимических — данные о собственных именах, фамилиях, прозвищах.

Толкование слов онлайн: кратчайший путь к знаниям

Проще изъясняться, конкретно и более ёмко выражать мысли, оживить свою речь, — все это осуществимо с расширенным словарным запасом. С помощью ресурса How to all вы определите значение слов онлайн, подберете родственные синонимы и пополните свою лексику. Последний пункт легко восполнить чтением художественной литературы. Вы станете более эрудированным интересным собеседником и поддержите разговор на разнообразные темы. Литераторам и писателям для разогрева внутреннего генератора идей полезно будет узнать, что означают слова, предположим, эпохи Средневековья или из философского глоссария.

Глобализация берет свое. Это сказывается на письменной речи. Стало модным смешанное написание кириллицей и латиницей, без транслитерации: SPA-салон, fashion-индустрия, GPS-навигатор, Hi-Fi или High End акустика, Hi-Tech электроника. Чтобы корректно интерпретировать содержание слов-гибридов, переключайтесь между языковыми раскладками клавиатуры. Пусть ваша речь ломает стереотипы. Тексты волнуют чувства, проливаются эликсиром на душу и не имеют срока давности. Удачи в творческих экспериментах!

Проект how-to-all.com развивается и пополняется современными словарями с лексикой реального времени. Следите за обновлениями. Этот сайт помогает говорить и писать по-русски правильно. Расскажите о нас всем, кто учится в универе, школе, готовится к сдаче ЕГЭ, пишет тексты, изучает русский язык.

ромб — Викисловарь

Морфологические и синтаксические свойства

ромб

Существительное, неодушевлённое, мужской род, 2-е склонение (тип склонения 1a по классификации А. А. Зализняка).

Корень: -ромб- ^{[Тихонов, 1996]}.

Произношение

МФА: ед. ч. [romp], мн. ч. [ˈrombɨ]

Семантические свойства

Значение

геометр. четырёхугольник, у которого все четыре стороны равны ◆ Всякий ромб является параллелограммом, но не наоборот.

Синонимы

уменьш. -ласк.: ромбик

Антонимы

Гиперонимы

параллелограмм, трапеция, дельтоид, четырёхугольник, многоугольник, геометрическая фигура

Гипонимы

квадрат

Родственные слова

Этимология

Происходит от др.-греч. ῥόμβος «кубарь, ромб», далее из праиндоевр. *werp- «крутить, вертеть». В ряде европейских языков слово заимств. через лат. rhombus. Русск. ромб, стар. ромбус — начиная с Штурма, 1709 г. Первое — из франц. rhombe, а форма на -ус — из нем. или лат. Использованы данные словаря М. Фасмера. См. Список литературы.

Фразеологизмы и устойчивые сочетания

Перевод

Анаграммы

Библиография

Морфологические и синтаксические свойства

ромб

Существительное, мужской род.

Корень: —.

Произношение

Семантические свойства

Значение

ромб (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы

Антонимы

Гиперонимы

Гипонимы

Родственные слова

Ближайшее родство

Этимология

Происходит от др.-греч. ῥόμβος «кубарь, ромб», далее из праиндоевр. *werp- «крутить, вертеть». В ряде европейских языков слово заимств. через лат. rhombus.

Фразеологизмы и устойчивые сочетания

Морфологические и синтаксические свойства

Ед.	ро́мб
Ед. об.	ро́мба
Ед. суб.	ро́мбът
Мн.	ро́мбове
Мн. сов.	ро́мбовете
Числ.	ро́мба
Зв.	—

ромб

Существительное, мужской род, склонение 1.

Корень: —.

Произношение

Семантические свойства

Значение

ромб (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы

Антонимы

Гиперонимы

четириъгълник, многоъгълник

Гипонимы

квадрат

Родственные слова

Ближайшее родство

Этимология

Фразеологизмы и устойчивые сочетания

Морфологические и синтаксические свойства

ромб

Существительное, мужской род.

Корень: —.

Произношение

Семантические свойства

Значение

ромб (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы

Антонимы

Гиперонимы

Гипонимы

квадрат

Родственные слова

Ближайшее родство

Этимология

Фразеологизмы и устойчивые сочетания

Морфологические и синтаксические свойства

ромб

Существительное, мужской род.

Корень: —.

Произношение

Семантические свойства

Значение

ромб (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы

Антонимы

Гиперонимы

Гипонимы

квадрат

Родственные слова

Ближайшее родство

Этимология

Фразеологизмы и устойчивые сочетания

Морфологические и синтаксические свойства

ромб

Существительное, неодушевлённое, мужской род.

Корень: —.

Произношение

Семантические свойства

Значение

ромб (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы

Антонимы

Гиперонимы

многокутник

Гипонимы

квадрат

Родственные слова

Ближайшее родство

Этимология

Фразеологизмы и устойчивые сочетания

Его свойства, форма, диагонали, стороны и формула площади

Вероятно, самый известный ромб – это бейсбольный алмаз. Расстояние между каждой базой одинаковое, Делаем форму ромба!

Еще больше интересных математических фактов!

Ромб – это разновидность параллелограмма, и что отличает его форму, так это то, что все четыре его стороны конгруэнтный.

Есть несколько формул ромба, которые имеют отношение к его:

Стороны (подробнее нажмите)
Все 4 стороны совпадают.
Уголки
Диагонали делят углы при вершинах пополам.
Диагонали
Диагонали перпендикулярны.
Площадь

Квадрат – это ромб?

Ответ:

Да, квадрат – это ромб

Квадрат должен иметь 4 равные стороны.У каждого ромба 4 совпадающих стороны, поэтому каждый квадрат также является ромбом. Квадрат – это особый ромб, у которого также четыре прямых угла.

Имейте в виду, что вопрос “Является ли квадрат ромбом?” означает Всегда ли каждый квадрат является ромбом?

Ромб – это квадрат?

Ответ:
Нет, ромб не квадрат
У квадрата должно быть 4 прямых угла. С другой стороны, у ромба нет никаких правил относительно его углов, поэтому существует множество примеров ромба, которые не являются квадратами.
Имейте в виду, что вопрос «Ромб – это квадрат?» означает Всегда ли каждый ромб квадрат?
Диаграмма 2
Как вы можете видеть на диаграмме 2, можно создать ромб, который не является квадратом.
Калькулятор ромбов
Что такое площадь и периметр ромба?
Четырехугольник с четырьмя равными сторонами представляет собой ромб или ромб (см. Рисунок ниже).В некоторой литературе его называют равносторонним четырехугольником, так как все его стороны равны по длине.
Это означает, что если $ {\ overline {AB}} \ cong {\ overline {BC}} \ cong {\ overline {CD}} \ cong {\ overline {DA}} $, то $ {\ overline {ABCD}} $ – это ромб. Поскольку противоположные стороны параллельны, ромб является параллелограммом, но не каждый параллелограмм является ромбом. Это означает, что все свойства параллелограмма можно применить и к ромбу. Напомним, параллелограмм обладает следующими свойствами:
Противоположные стороны параллелограмма равны;
Противоположные углы параллелограмма равны;
Последовательные углы параллелограмма дополняют друг друга;
Диагонали параллелограмма делят друг друга пополам
Ромб обладает еще двумя свойствами:
Диагонали делят пополам противоположные углы ромба;
Диагонали ромба перпендикулярны.
Любой четырехугольник с перпендикулярными диагоналями, одна диагональ которой пересекает другую, является воздушным змеем. Итак, ромб – это воздушный змей, но не каждый воздушный змей – ромб. Любой четырехугольник, который одновременно является воздушным змеем и параллелограммом, является ромбом. Поскольку диагонали ромба перпендикулярны, мы можем применить теорему Пифагора, чтобы найти длину стороны ромба. Рассмотрим ромб $ \ overline {ABCD} $. Диагонали ромба пересекают друг друга пополам, $ \ overline {AO} \ cong \ overline {OC} $ и $ \ overline {BO} \ cong \ overline {OD}.o $ вращение против часовой стрелки вокруг точки $ O $ переводит ромб в себя.
Расстояние вокруг ромба называется периметром ромба. Обычно обозначается $ P $. Чтобы найти периметр ромба, складываем длины его сторон. Таким образом, периметр ромба с длиной стороны $ a $ равен
$$ P = a + a + a + a = 4 \ times a $$
. Площадь ромба – это количество квадратных единиц, необходимое для заполнения ромба. Площадь, обычно обозначаемая $ A $. Ромб и прямоугольник на одном основании и между одинаковыми параллелями равны по площади.2) $ и т. Д.
Площадь и периметр ромба со ступенями показывает полный пошаговый расчет для определения периметра и площади ромба с длиной стороны $ 10 \; in $ и мерой угла. 30 долларов по формулам периметра и площади. Для любых других значений длины стороны и меры угла ромба просто введите два положительных вещественных числа и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать эту область и периметр ромба для создания работы, проверки результатов периметра и площади двумерных фигур или эффективного выполнения домашних заданий.
Rhombus – определение математического слова
Rhombus – определение математического слова – Math Open Reference Попробуйте это Перетащите оранжевые точки на каждую вершину чтобы изменить форму ромба. Обратите внимание, что четыре стороны остаются одинаковой длины, а противоположные стороны остаются параллельными.
На самом деле ромб – это просто особый тип параллелограмма. Напомним, что в параллелограмме все пары противоположных сторон равны по длине. У ромба все четыре стороны имеют одинаковую длину.Следовательно, он обладает всеми свойствами параллелограмма. См. Определение параллелограмма
Это немного похоже на квадрат, который может “ наклониться ” и внутренние углы , а не должны быть 90 °. Иногда ее называют ромбовидной или ромбовидной формы.
Свойства ромба
.
База Базой можно считать любую сторону. Выбирайте любой понравившийся. Если используется для расчета площади (см. Ниже), необходимо использовать соответствующую высоту. На рисунке выше выбрана одна из четырех возможных баз.
Высота Высота ромба – это расстояние по перпендикуляру. от основания на противоположную сторону (которую, возможно, придется расширить). На рисунке выше показана высота, соответствующая базовому CD.
Площадь Есть несколько способов найти площадь ромба. Чаще всего используется (база × высота). Каждый описан в Области ромба
Периметр Расстояние вокруг ромба.Сумма длин сторон. См. Периметр ромба
Диагонали Каждая из двух диагоналей – это серединный перпендикуляр другого. См. Диагонали ромба
Другие темы полигонов
Общие
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные многоугольники
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Формула площади ромба с калькулятором
Формула площади ромба с калькулятором – Math Open Reference Три разных способа рассчитать площадь ромбы приведены ниже, с формулой для каждого.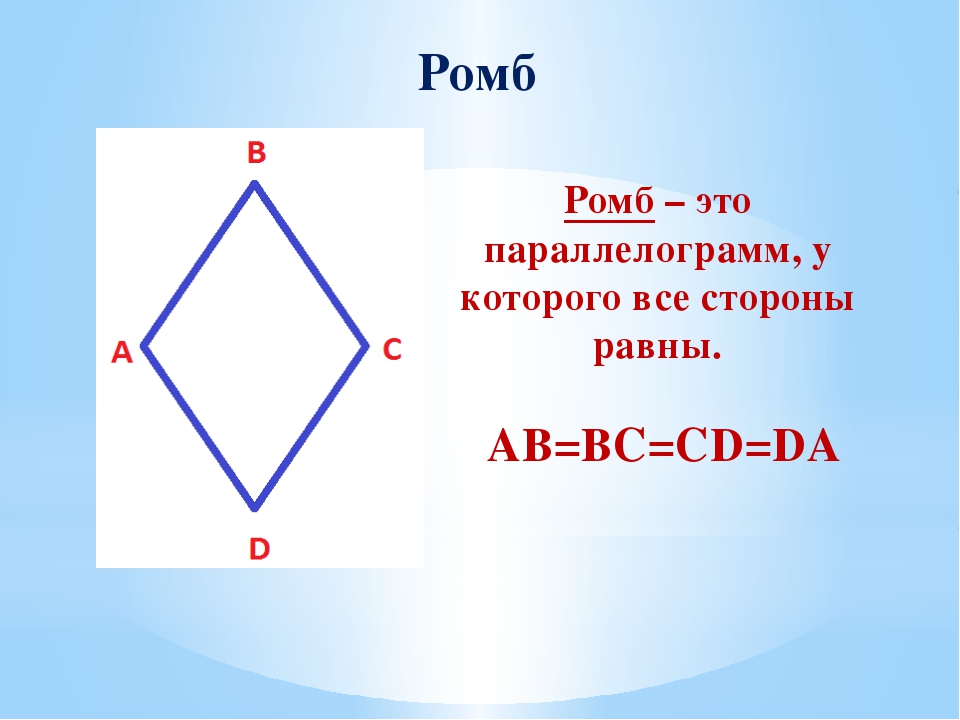 Попробуйте это Перетащите оранжевые точки на каждую вершину чтобы изменить форму ромба. Площадь будет постоянно рассчитываться с использованием метода «базисное умножение на высоту».
Ромб на самом деле это просто особый тип параллелограмма.К ним также можно применить многие расчеты площади. Выберите формулу на основе значений, которые вам известны для начала.
1. Метод “базис, умноженный на высоту”
Сначала выберите одну сторону в качестве основы. Подойдет любой, все они одинаковой длины. Затем определите высоту – перпендикулярное расстояние от выбранной базы до противоположной стороны. Площадь – это произведение этих двух или, как формула: где
b – длина основания
a – высота (высота).
Воспользуйтесь калькулятором ниже, чтобы вычислить площадь ромба с учетом длины основания (стороны) и высота (перпендикулярная высота).
Введите любые два значения, и будет вычислено недостающее. Например, введите площадь и базовую длину, и будет рассчитана высота, необходимая для получения этой площади.
2. Метод «диагоналей»
Еще одна простая формула для определения площади ромба, когда известны длины диагоналей. Площадь составляет половину произведения диагоналей.В виде формулы: где
d ₁ – длина диагонали
d ₂ – длина другой диагонали
3. Использование тригонометрии
Если вы знакомы с тригонометрией, есть удобная формула, когда вы знаете длину стороны и любой угол: где
s – длина любой стороны
a – любой внутренний угол
sin – синусоидальная функция
(см. Обзор тригонометрии)
Поначалу может показаться странным, что вы можете использовать любой угол, поскольку не все они равны.Но углы либо равны, либо дополнительный, и дополнительные углы имеют одинаковый синус.
Другие темы полигонов
Общие
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные многоугольники
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
прямоугольников, ромбов и квадратов | Ресурсы Wyzant
По мере того, как мы продвигались четырехугольников, мы стали все более и более конкретизировать тип фигур, с которыми мы имеем дело.Сначала мы рассматривали всевозможные полигоны, а потом мы сузили его до четырехугольников, называемых четырехугольниками. Оттуда мы узнал об особом типе четырехугольника, противоположные стороны которого параллельны, называется параллелограмм. В этом разделе мы станем еще более конкретными, изучив свойства различных параллелограммов. Давайте узнаем, что делает прямоугольники, ромбы и квадраты особые фигуры.
Прямоугольники
Определение: Прямоугольник – это четырехугольник с четырьмя прямыми углами.
Обратите внимание, что мы используем «четырехугольник» в нашем определении прямоугольников. Мы могли бы иметь также сказал, что прямоугольник – это параллелограмм с четырьмя прямыми углами, поскольку и четырехугольник с четырьмя прямыми углами также является параллелограммом (потому что их противоположные стороны будут параллельны).
Прямоугольники обладают парой свойств, которые помогают отличить их от других параллелограммов. Изучая эти свойства, мы сможем различать различные типы параллелограммов и классифицируйте их более конкретно. Имейте в виду, что все фигуры в этом разделе имеют общие свойства параллелограммов. То есть все они иметь
(1) противоположных сторон, которые параллельны,
(2) конгруэнтных противоположных углов,
(3) противоположных сторон, которые совпадают,
(4) последовательных углов, которые являются дополнительными, и
(5) диагоналей, пересекающих друг друга.
Теперь давайте посмотрим на свойства, которые делают прямоугольники особым типом параллелограмма.
(1) Все четыре угла прямоугольника – прямые.
(2) Диагонали прямоугольника совпадают.
Ромбы
Определение: Ромб – это четырехугольник с четырьмя конгруэнтными сторонами.
Подобно определению прямоугольника, мы могли бы использовать слово «параллелограмм». вместо «четырехугольника» в нашем определении ромба. Таким образом, у ромбов есть все свойств параллелограммов (указанных выше), а также некоторые другие. Давайте посмотрите на эти свойства.
(1) Последовательные стороны ромба равны.
(2) Диагонали ромба делят пополам пары противоположных углов.
(3) Диагонали ромба перпендикулярны.
Квадраты
Определение: Квадрат – это параллелограмм с четырьмя равными сторонами и четырьмя конгруэнтные углы.
Обратите внимание, что определение квадрата – это комбинация определений прямоугольник и ромб.Следовательно, квадрат – это и прямоугольник, и ромб, что означает, что свойства параллелограммов, прямоугольников и ромбов все применить к квадратам. Поскольку квадраты обладают комбинацией всех этих различных свойств, это очень специфический тип четырехугольника.
Посмотрите на иерархию четырехугольников ниже. Этот рисунок показывает прогрессию наших знаний о многоугольниках, начиная с четырехугольников и заканчивая квадратами.
Обратите внимание на две стрелки, указывающие на квадрат. Это потому, что квадрат обладает всеми свойствами прямоугольника и ромба.
Теперь, когда мы знаем о свойствах прямоугольников, ромбов и квадратов, давайте поработайте над несколькими упражнениями, которые позволят оценить наше понимание этого материала.
Упражнение 1
Обозначьте каждый параллелограмм как прямоугольник, ромб или квадрат.
Ответ:
Во-первых, давайте взглянем на параллелограмм A. На рисунке показано, что у него четыре конгруэнтных стороны и что его диагонали пересекаются перпендикулярно. Потому что его стороны совпадают, мы знаем, что параллелограмм не является прямоугольником. Тот факт, что параллелограмм А пересечение диагоналей перпендикулярно нам не помогает, потому что и ромбы, и квадраты разделяют эту характеристику.Угол в вершине параллелограмма A не равен но под прямым углом. Следовательно, мы знаем, что это не квадрат. Параллелограмм А – ромб.
В параллелограмме B мы видим, что есть четыре прямых угла и что пары противоположные стороны конгруэнтны. Однако последовательные стороны не совпадают, поэтому мы можем исключить из наших вариантов ромбы и квадраты. Таким образом, параллелограмм B является прямоугольник.
Давайте теперь посмотрим на параллелограмм C. Отметим, что он имеет пару прямых углов и четыре конгруэнтных стороны. Наша склонность заставляет нас думать, что этот параллелограмм квадрат, но давайте на всякий случай убедимся. Мы знаем, что два прямых угла данные нам имеют сумму 180 ° . Поскольку внутренние углы четырехугольника это 360 ° , мы знаем, что оставшиеся два угла должны иметь сумму 180 ° (потому что 360-180 = 180 ).Противоположные углы параллелограммов конгруэнтны, что означает, что недостающие углы должны иметь меру из 90 ° (начиная с 180 ÷ 2 = 90 ). Это говорит нам, что есть на самом деле четыре прямых угла в параллелограмме C, поэтому мы знаем, что это квадрат (и ромб).
Упражнение 2
Найдите значение x для прямоугольника ABCD ниже.
Ответ:
Мы знаем, что ABCD – это прямоугольник, поэтому давайте воспользуемся некоторыми свойствами прямоугольника. чтобы помочь нам понять, что такое x .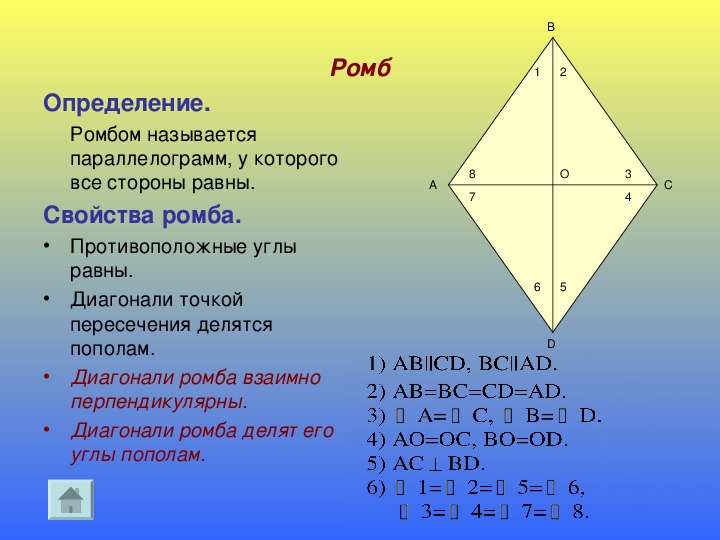 Кажется, что в центре внимания это упражнение по диагоналям фигуры. Сверху мы знаем, что диагонали прямоугольника конгруэнтны, поэтому давайте установим сегменты AC и BD равны между собой:
Итак, получаем x = 12 .
Упражнение 3
Ответ:
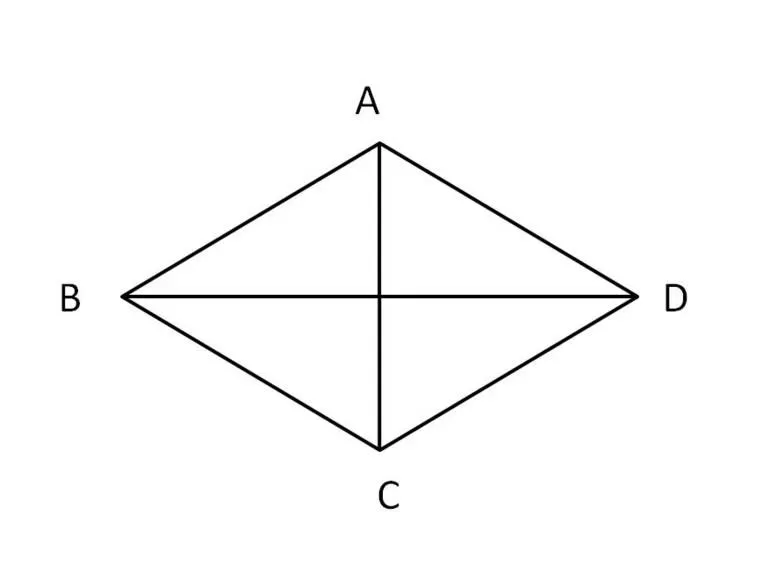
Давайте рассмотрим информацию, полученную в результате упражнения, чтобы вывести из него больше информации. Мы знаем, что EKIN – параллелограмм, и что ? 1 ?? 2 . Поскольку EKIN – параллелограмм, мы знаем, что что его противоположные стороны параллельны. Следовательно, сегменты EK и В параллельны.
Затем мы можем использовать теорему об альтернативных внутренних углах , чтобы утверждать, что ? 1 ?? 4 и ? 2 ?? 3 . Напомним, что альтернативные внутренние углы совпадают. тогда и только тогда, когда трансверсаль пересекает пару параллельных прямых. В этом случае, наша пара параллельных линий: EK и IN , а наша поперечная сегмент НК .
По транзитивности можно сказать, что ? 1 ?? 3 и ? 2 ?? 4 . Давайте посмотрите на нашу цепочку сравнений, чтобы убедиться, что предыдущие утверждения правда.
Диагональ делит наш параллелограмм на два треугольника. Фактически, потому что два угла каждого треугольника совпадают, можно сказать, что ? EKN и ? INK – равнобедренные треугольники. Обратное теореме о равнобедренном треугольнике утверждает что стороны, противоположные конгруэнтным углам равнобедренных треугольников, совпадают, поэтому мы знаем, что сегмент EK соответствует сегменту EN , и что сегменты IK и IN совпадают.
Теперь можно сказать, что сегменты EK и IN совпадают, как EN и IK , потому что противоположные стороны параллелограмма конгруэнтны.По транзитивности мы знаем, что EN? EK? IN? IK . Давайте смотреть на нашей новой иллюстрации.
Таким образом, параллелограмм EKIN является ромбом, потому что он имеет четыре равных стороны. Наши Геометрическое доказательство этого упражнения из двух столбцов показано ниже.
Упражнение 4
Каким должно быть значение y , чтобы ромб PQRS был квадратом?
Ответ:
Прежде чем мы сможем вычислить наши y , мы должны определить, какое значение х есть.В конечном итоге мы хотим, чтобы ромб PQRS был квадратом, это означает, что PQRS должно иметь четыре прямых угла.
Давайте начнем с выяснения, что такое x . Это относительно просто, потому что мы можем просто установить сегмент PQ равным PS :
Теперь, когда мы знаем, что такое x , мы можем подставить его в меру угла, данного нас. Но сначала нам нужно выяснить, какова общая величина ? QSR . Мы знаем что мы хотим, чтобы ? PSR было 90 ° . Также мы знаем, что диагонали квадрата пополам пары противоположных углов. Следовательно, ? PSR следует разделить пополам на сегмент QS , разделив угол вверх на два равных угла 45 ° (потому что 90 ÷ 2 = 45 ).Теперь мы можем установить ? QSR равно 45 ° . Получаем:
Теперь мы заменяем 7 на x :
Таким образом, значение y должно быть 4 , чтобы ромб PQRS также был квадратом.
Программа на Java для расчета площади ромба
Программа на Java для определения площади ромба или вычисления площади ромба. Мы также добавили онлайн-компилятор и инструмент выполнения , чтобы проверить программу на соответствие вашим значениям. Было так много способов найти / вычислить.
Что такое ромб?
Ромб представляет собой плоскую форму, у которой все стороны равны по длине, а противоположные стороны равны и углы.
Какая формула?
Может быть очень много способов найти площадь ромба. Здесь мы делимся простой формулой. Проверить это.
(диагональ (D1) * диагональ (D2) / 2)
[wp_ad_camp_3]
Вот пример программы, метод -1 # Инструмент онлайн-выполнения # Java-программа для поиска области ромба #
1
2
3
4
5
6
7
8
9
10
11
12
13
140002
14
импорт java. util.Scanner;
class AreaOfRhombus
{
public static void main (String args [])
{
Scanner s = new Scanner (System.in);
System.out.println («Введите диагональ 1:»);
двойной d1 = s.nextDouble ();
System.out.println («Введите диагональ 2:»);
двойной d2 = s.nextDouble ();
двойная площадь = (d1 * d2) / 2;
Система.out.println («Площадь ромба равна:» + площадь);
}
}
Выход:
Введите диагональ 1:
15
Введите диагональ 2:
18
Площадь ромба: 135,0
Инструмент онлайн-исполнения для вышеуказанного кода ромба:
Насколько просто это было правильно? Если вы новичок в программировании на Java и не знаете, как работает указанная выше программа, ознакомьтесь с приведенным ниже руководством по программе Java.
Объяснение кода:
import java.util.Scanner;
– который считывает входные значения из основной системы и передает их в код основного блока или считает, что он имеет основу для программы. Функция сканера основного блока будет использовать основные методы из пакета JDK.
– это план, в котором объекты создаются внутри класса.
Сканер s = новый сканер (System.in);
– Сканер – это метод, который считывает входные значения из системы. И system.in – это функция, которая может считывать значения из вашей системы (import.java.util.Scanner).
.