Разное

Симметричные звезды: Hot or not? Как бы выглядели звезды, если бы их лица были абсолютно симметричны

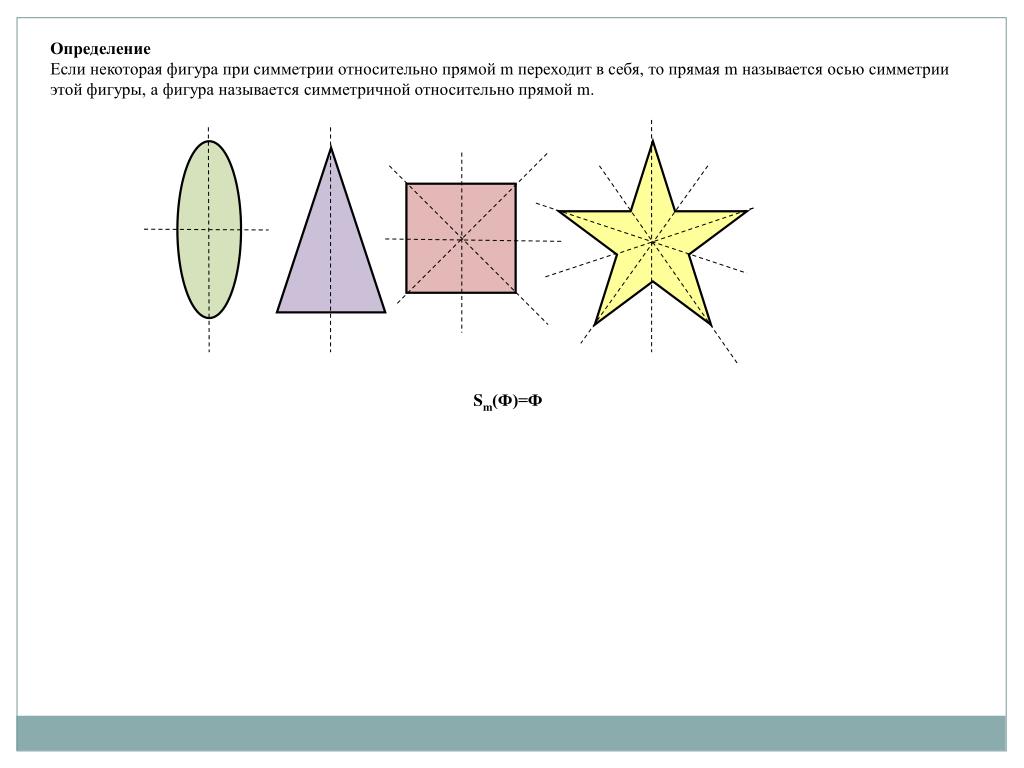
ЗВЁЗДНАЯ ДИНАМИКА • Большая российская энциклопедия

Авторы: А. С. Расторгуев

ЗВЁЗДНАЯ ДИНА́МИКА (ди­на­ми­ка звёзд­ных сис­тем), изу­ча­ет за­ко­но­мер­но­сти дви­же­ния звёзд в гра­ви­та­ци­он­ном по­ле звёзд­ной сис­те­мы и эво­лю­цию звёзд­ных сис­тем. З. д. ис­сле­ду­ет пар­ное и кол­лек­тив­ное гра­ви­тац. взаи­мо­дей­ст­вия звёзд, рав­но­вес­ные со­стоя­ния звёзд­ных сис­тем и их ди­на­мич. эво­лю­цию под влия­ни­ем как внут­рен­них, так и внеш­них фак­то­ров. Осо­бое ме­сто в З. д. при­над­ле­жит са­мо­гра­ви­ти­рую­щим сис­те­мам, в ко­то­рых ка­ж­дая звез­да дви­жет­ся в об­щем гра­ви­тац. по­ле, соз­дан­ном все­ми звёз­да­ми сис­те­мы. З. д. тес­но свя­за­на с не­бес­ной ме­ха­ни­кой, гид­ро­ди­на­ми­кой, ста­ти­стич. фи­зи­кой, ана­ли­тич. ме­ха­ни­кой, ки­не­тич. тео­ри­ей га­зов.

Ос­но­вы З. д. бы­ли за­ло­же­ны в 1915–1920 Дж. Джин­сом и А. Эд­динг­то­ном, а позд­нее В. А. Ам­бар­цу­мя­ном и С. Чан­д­ра­се­ка­ром. В 1920–30-х гг. Б. Линд­блад вы­вел осн. ди­на­мич. со­от­но­ше­ния для Га­лак­ти­ки.

Мак­ро­ско­пич. со­стоя­ние звёзд­ной сис­те­мы опи­сы­ва­ет­ся функ­ци­ей фа­зо­вой плот­но­сти, имею­щей смысл функ­ции рас­пре­де­ле­ния в шес­ти­мер­ном фа­зо­вом про­стран­ст­ве и за­ви­ся­щей от ко­ор­ди­нат и ско­ро­стей звёзд. Для удоб­ст­ва опи­са­ния гра­ви­тац. си­ла, дей­ст­вую­щая на звез­ду, пред­став­ля­ет­ся в ви­де сум­мы ре­гу­ляр­ной си­лы, обу­слов­лен­ной сгла­жен­ным рас­пре­де­ле­ни­ем плот­но­сти, и ир­ре­гу­ляр­ной си­лы, воз­ни­каю­щей при тес­ных сбли­же­ни­ях звёзд. Под дей­ст­ви­ем ре­гу­ляр­ной си­лы звез­да дви­жет­ся по ре­гу­ляр­ной ор­би­те, в то вре­мя как сбли­же­ния звёзд, рас­смат­ри­вае­мые в рам­ках слу­чай­но­го про­цес­са, пред­став­ля­ют со­бой ис­точ­ник гра­ви­тац. воз­му­ще­ний ор­би­ты. От­но­си­тель­ная роль ре­гу­ляр­ных и ир­ре­гу­ляр­ных сил за­ви­сит от ста­дии эво­лю­ции сис­те­мы; для ква­зи­ста­цио­нар­ных сис­тем (ха­рак­те­ри­сти­ки ко­то­рых мед­лен­но ме­ня­ют­ся со вре­ме­нем) роль ир­ре­гу­ляр­ных сил рас­тёт с умень­ше­ни­ем чис­ла звёзд в сис­те­ме.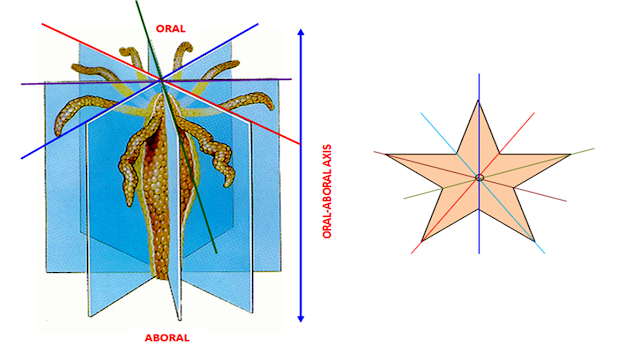 Ир­ре­гу­ляр­ные си­лы, из­ме­няя ско­ро­сти звёзд, ве­дут к ус­та­нов­ле­нию рав­но­вес­но­го рас­пре­де­ле­ния ско­ро­стей, т. е. обес­пе­чи­ва­ют ме­ха­низм столк­но­ви­тель­ной ре­лак­са­ции за счёт сбли­же­ний звёзд. Для рас­се­ян­ных звёзд­ных ско­п­ле­ний вре­мя ре­лак­са­ции со­став­ля­ет 1–10 млн. лет, для ти­пич­ных ша­ро­вых ско­п­ле­ний – 100 млн. – 10 млрд. лет, в дис­ке Га­лак­ти­ки вре­мя ре­лак­са­ции при­мер­но в 10 тыс. раз боль­ше воз­рас­та Все­лен­ной. Это оз­на­ча­ет, что вза­им­ные сбли­же­ния звёзд мо­гут иг­рать за­мет­ную роль толь­ко в ди­на­ми­ке рас­се­ян­ных и ша­ро­вых звёзд­ных ско­п­ле­ний и эти сис­те­мы мо­гут на­хо­дить­ся в ква­зи­ста­цио­нар­ном со­стоя­нии по от­но­ше­нию к ир­ре­гу­ляр­ным си­лам. Га­лак­ти­ка в це­лом и др. круп­ные звёзд­ные сис­те­мы мо­гут счи­тать­ся бес­столк­но­ви­тель­ны­ми звёзд­ны­ми сис­те­ма­ми. Столк­но­ви­тель­ная ре­лак­са­ция ве­дёт к по­яв­ле­нию звёзд со ско­ро­стя­ми, пре­вы­шаю­щи­ми ско­рость ухо­да, и, сле­до­ва­тель­но, к по­те­ре мас­сы звёзд­ной сис­те­мой. Гру­бая оцен­ка по­ка­зы­ва­ет, что за вре­мя ре­лак­са­ции сис­те­му по­ки­да­ет ок. 1% звёзд. По­те­ря мас­сы – гл. фак­тор ди­на­мич. эво­лю­ции звёзд­ных сис­тем. Про­стей­шая мо­дель ди­на­мич. эво­лю­ции пред­ска­зы­ва­ет пол­ный рас­пад звёзд­но­го ско­п­ле­ния за 20–40 на­чаль­ных вре­мён ре­лак­са­ции.

В от­ли­чие от мно­гих рас­смат­ри­вае­мых в фи­зи­ке сис­тем час­тиц, звёзд­ная сис­те­ма прин­ци­пи­аль­но не­ста­цио­нар­на, по­сколь­ку от­сут­ст­вие гра­ниц де­ла­ет не­из­беж­ной по­те­рю звёзд. Од­на­ко мед­лен­ный темп по­те­ри мас­сы по­зво­ля­ет счи­тать звёзд­ную сис­те­му ква­зи­ста­цио­нар­ной поч­ти на всём ин­тер­ва­ле её вре­ме­ни жиз­ни, за ис­клю­че­ни­ем крат­ко­вре­мен­но­го на­чаль­но­го пе­рио­да пе­ре­хо­да сис­те­мы в ква­зи­рав­но­вес­ное со­стоя­ние, ко­гда эво­лю­ция звёзд­ной сис­те­мы управ­ля­ет­ся гл. обр. бы­ст­рым из­ме­не­ни­ем об­ще­го гра­ви­тац. по­тен­циа­ла (ста­дия «бур­ной» ре­лак­са­ции). За это вре­мя со­вме­ст­ное дей­ст­вие столк­но­ви­тель­ной ре­лак­са­ции и бы­строе из­ме­не­ние гра­ви­тац. по­тен­циа­ла сис­те­мы при­во­дят её в со­стоя­ние, близ­кое к рав­но­вес­но­му в ре­гу­ляр­ном по­ле.

Изу­че­ние строе­ния и ди­на­ми­ки ква­зи­рав­но­вес­ных сис­тем – од­но из важ­ней­ших на­прав­ле­ний З. д. Ди­на­ми­ка та­ких сис­тем опи­сы­ва­ет­ся урав­не­ни­ем Больц­ма­на для функ­ции фа­зо­вой плот­но­сти. В пре­неб­ре­же­нии ир­ре­гу­ляр­ны­ми си­ла­ми ис­поль­зу­ет­ся бес­столк­но­ви­тель­ное урав­не­ние Больц­ма­на. Ди­на­мич. эво­лю­ция звёзд­ных сис­тем, в ко­то­рых су­ще­ст­вен­ную роль иг­ра­ют сбли­же­ния звёзд, опи­сы­ва­ет­ся урав­не­ни­ем Больц­ма­на со столк­но­ви­тель­ным чле­ном. В бо­га­тых звёзд­ных сис­те­мах отд. пар­ные сбли­же­ния звёзд при­во­дят к очень ма­лым из­ме­не­ни­ям их ско­ро­стей. Для учё­та эф­фек­та на­ко­п­ле­ния ма­лых не­за­ви­си­мых слу­чай­ных из­ме­не­ний (ку­му­ля­тив­но­го эф­фек­та) ис­поль­зу­ет­ся урав­не­ние Фок­ке­ра – План­ка. На­про­тив, в не­боль­ших звёзд­ных сис­те­мах, где воз­мож­ны сбли­же­ния с боль­ши­ми из­ме­не­ния­ми ско­ро­сти, столк­но­ви­тель­ный член име­ет вид урав­не­ния Кол­мо­го­ро­ва – Фел­ле­ра.

Боль­шое тео­ре­тич. и прак­тич. зна­че­ние для З. д. име­ет ви­риа­ла тео­ре­ма, вы­ра­жаю­щая связь меж­ду ки­не­ти­че­ской $T$ и по­тен­ци­аль­ной $Ω$ энер­гия­ми эво­лю­цио­ни­рую­щей ква­зи­ста­цио­нар­ной звёзд­ной сис­те­мы: $2T + Ω =0$. Её след­ст­вие – тре­бо­ва­ние от­ри­ца­тель­но­сти пол­ной энер­гии сис­те­мы как не­об­хо­ди­мо­го ус­ло­вия её гра­ви­тац. ус­той­чи­во­сти. На ос­но­ве тео­ре­мы ви­риа­ла вы­во­дят­ся ди­на­мич. оцен­ки масс звёзд­ных ско­п­ле­ний и ско­п­ле­ний га­лак­тик и вы­чис­ля­ют­ся свя­зи ме­ж­ду их мак­ро­ско­пич. ха­рак­те­ри­сти­ка­ми. Тео­ре­ма ви­риа­ла по­зво­ля­ет оп­ре­де­лить на­прав­ле­ние ди­на­мич. эво­лю­ции звёзд­ных сис­тем: по­те­ря мас­сы и пол­ной энер­гии со­про­во­ж­да­ет­ся рос­том кон­цен­тра­ции мас­сы и уве­ли­че­ни­ем дис­пер­сии ско­ро­стей.

Прак­ти­че­ски все звёзд­ные сис­те­мы на­хо­дят­ся во внеш­нем гра­ви­тац. по­ле. На звёзд­ные ско­п­ле­ния дей­ст­ву­ют при­лив­ные си­лы со сто­ро­ны Га­лак­ти­ки, ус­ко­ряю­щие темп по­те­ри звёзд и ди­на­мич. эво­лю­цию ско­п­ле­ний. Дви­га­ясь по га­лак­тич. ор­би­там, звёзд­ные ско­п­ле­ния сво­им тя­го­те­ни­ем вы­зы­ва­ют гра­ви­тац. фо­ку­си­ров­ку звёзд га­лак­тич. фо­на по­за­ди скоп­ле­ния, тор­мо­зя­щую их дви­же­ние. Этот эф­фект на­зы­ва­ет­ся ди­на­мич. тре­ни­ем, и он осо­бен­но силь­но ме­ня­ет ор­би­ты мас­сив­ных ша­ро­вых ско­п­ле­ний и спут­ни­ков Га­лак­ти­ки. Те­ряя энер­гию, они пе­ре­хо­дят на низ­кие га­лак­тич. ор­би­ты, где ус­ко­рен­но раз­ру­ша­ют­ся при­лив­ны­ми си­ла­ми. Сле­ды раз­ру­ше­ния кар­ли­ко­вых спут­ни­ков Га­лак­ти­ки хо­ро­шо вид­ны в тол­стом дис­ке Га­лак­ти­ки.

Ана­ли­тич. ме­то­ды ис­сле­до­ва­ния ди­на­мич. эво­лю­ции звёзд­ных сис­тем прин­ци­пи­аль­но ог­ра­ни­че­ны про­стей­ши­ми слу­чая­ми (напр., сфе­ри­че­ски-сим­мет­рич­ные ско­п­ле­ния звёзд оди­на­ко­вых масс), про­яс­няю­щи­ми наи­бо­лее об­щие за­ко­но­мер­но­сти ди­на­мич. эво­лю­ции. Боль­ших ус­пе­хов в кон. 20 – нач. 21 вв. дос­тиг­ло чис­лен­ное мо­де­ли­ро­ва­ние ди­на­ми­ки звёзд­ных сис­тем, со­стоя­щих из боль­шо­го чис­ла звёзд. Мо­де­ли­ро­ва­ние сво­дит­ся к пря­мо­му ин­те­гри­ро­ва­нию урав­не­ний дви­же­ния ка­ж­дой звез­ды в гра­ви­тац. по­ле, соз­да­вае­мом как её бли­жай­ши­ми со­се­дя­ми, так и все­ми звёз­да­ми. Чис­лен­ное мо­де­ли­ро­ва­ние, не­смот­ря на зна­чит. слож­но­сти, по­зво­ля­ет пре­одо­леть при­су­щие ана­ли­тич. ме­то­дам ог­ра­ни­че­ния и ис­сле­до­вать реа­ли­стич. звёзд­ные ско­п­ле­ния, со­стоя­щие из звёзд раз­ной мас­сы, учи­ты­вать их фи­зич. эво­лю­цию и ре­аль­ное га­лак­тич. ок­ру­же­ние. Осн. чер­той мно­го­числ. ме­то­дов пря­мых рас­чё­тов яв­ля­ет­ся стро­гий учёт пар­ных взаи­мо­дей­ст­вий звез­ды с её бли­жай­ши­ми со­се­дя­ми и пред­став­ле­ние об­ще­го ре­гу­ляр­но­го гра­ви­тац. по­ля сгла­жен­ным рас­пре­де­ле­ни­ем мас­сы. Ус­пеш­но реа­ли­зо­ва­но мо­де­ли­ро­ва­ние сфе­ри­че­ски-сим­мет­рич­ных и пло­ских сис­тем, со­стоя­щих из мил­лио­нов час­тиц. Чис­лен­ное мо­де­ли­ро­ва­ние вы­яви­ло боль­шую ди­на­мич. роль тес­ных двой­ных звёзд, взаи­мо­дей­ст­вие ко­то­рых с оди­ноч­ны­ми звёз­да­ми спо­соб­но ос­та­но­вить кол­лапс ядер плот­ных звёзд­ных ско­п­ле­ний. Ис­сле­ду­ют­ся не­ус­той­чи­во­сти, воз­ни­каю­щие в га­лак­тич. дис­ках, ко­то­рые мо­гут ге­не­ри­ро­вать вол­ны плот­но­сти, а так­же ряд др. яв­ле­ний.

§60. Схема соединения «звездой» | Электротехника

Схема «звезда с нулевым проводом».

При соединении фазных обмоток источника трехфазного тока (например, генератора) по схеме «звезда с нулевым проводом» концы его трех обмоток соединяют в общий узел 0, который называется нулевой точкой, или нейтралью источника (рис. 206).

Рис. 206. Схема «звезда с нулевым проводом», направление в ней линейных и фазных токов и напряжений

Приемники электрической энергии объединяют в три группы ZA, ZB и Zc (фазы нагрузки), концы которых также соединяют в общий узел 0′ (нулевая точка, или нейтраль нагрузки). Обмотки источника соединяют с фазами нагрузки четырьмя проводами. Провода 1, 2 и 3, присоединенные к началам фазных обмоток (А, В, С), называют линейными. Провод 4, соединяющий нулевые точки 0 и 0′, называют нулевым, или нейтральным.

Напряжения uА, uв и u

с между началами и концами обмоток отдельных фаз источника или фаз нагрузки ZA, ZB и Zc называют фазными. Они равны также напряжениям между каждым из линейных проводов и нулевым проводом. При отсутствии потери напряжения в обмотках источника (при холостом ходе) фазные напряжения равны соответствующим э. д. с. в этих обмотках.

Фазными токами iA, iB, ic называют токи, протекающие по обмоткам источника или фазам нагрузки ZA, ZB и Zc. Напряжения uAB, uBC, uCA между линейными проводами и токи, проходящие по этим проводам, называют линейными.

Примем условно за положительное направление токов iA, iB и ic в фазах источника — от конца соответствующей фазы к ее началу,в фазах нагрузки — от начала к концу, а в линейных проводах — от источника к приемнику.

Будем считать положительными напряжения uА, uB и uC в фазах источника и нагрузки, если они направлены от начала фаз к концам, а линейные напряжения uАВ, uBC, uСА — если они направлены от предыдущей фазы к последующей.

Из рис. 206 следует, что в схеме «звезда» линейные токи равны фазным, т. е. Iл = Iф, так как при переходе от фазы источника или нагрузки к линейному проводу нет каких-либо ответвлений.

Мгновенные значения напряжений согласно второму закону Кирхгофа:

uАВ = uА – uB; uBC = uB – uС; uСА = uС – uА.

Переходя от мгновенных значений напряжений к их векторам, имеем:

Следовательно, линейное напряжение равно разности векторов соответствующих фазных напряжений

.

По полученным векторным уравнениям можно построить векторную диаграмму (рис.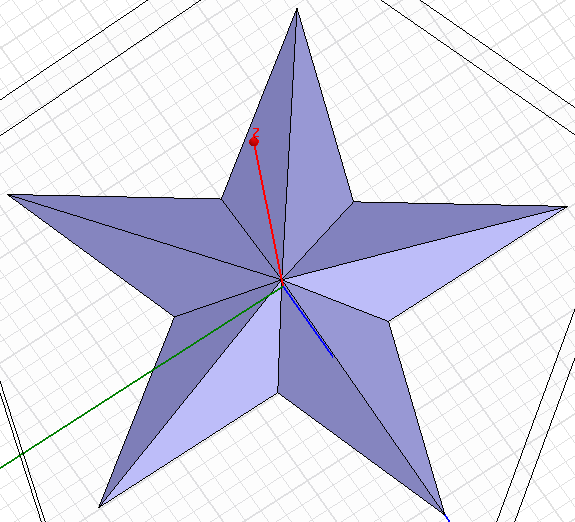 207, а), которую можно преобразовать в диаграмму (рис. 207,б). Из этой диаграммы видно, что в симметричной трехфазной системе векторы линейных напряжений →uAB, →uВС, →uСА образуют равносторонний треугольник ABC, внутри которого расположена симметричная трехлучевая звезда фазных напряжений →uА, →uВ, →uС.

В равнобедренных треугольниках АОВ, ВОС и СОА основание равно Uл две другие стороны — Uф и острый угол между этими сторонами и основанием составляет 30°.

Рис. 207. Векторные диаграммы напряжений для схемы «звезда с нулевым проводом»

Следовательно,

Uл = 2Uф cos 30° = 2Uф (√3)/2 = √3 U

ф

Таким образом, в трехфазной системе, соединенной по схеме «звезда с нулевым проводом», линейное напряжение больше фазного в √З раз. Величина √З = 1,73 положена в основу шкалы номинальных напряжений переменного тока: 127, 220, 380 и 660 В. В этом ряду каждое следующее значение напряжения больше предыдущего в 1,73 раза.

В нулевом проводе проходит ток i0, мгновенное значение которого равно алгебраической сумме мгновенных значений токов, проходящих в отдельных фазах: i0 = iA+iB+iC.

Переходя от мгновенных значений токов к их векторам, имеем:

→i0=→iA+→iB+→iC.

Векторы токов →iА, →iВ и →iС сдвинуты относительно векторов соответствующих напряжений →uA, →uB, →uС на углы →iA, →iB, →i

C (рис. 208, а). Значения этих углов зависят от соотношения между активным и реактивным сопротивлениями, включенными в данную фазу.

На этой же диаграмме показано сложение векторов →iА, →iВ и →iC для определения вектора тока →i0. Обычно ток →i0 меньше токов

Рис. 208. Векторные диаграммы напряжений и токов в отдельных фазах для схемы «звезда с нулевым проводом» при неравномерной (а) и равномерной (б) нагрузках фаз

IA, 1В и IC в линейных проводах, поэтому нулевой провод имеет площадь поперечного сечения, равную или даже несколько меньшую площади сечения линейных проводов.

В схеме «звезда с нулевым проводом» приемники электрической энергии можно включать на два напряжения: линейное U

л (при подключении к двум линейным проводам) и фазное UФ (при подключении к нулевому и одному из линейных проводов).

Схема «звезда без нулевого провода».

При равномерной или симметричной нагрузке всех трех фаз, когда во всех фазах включены одинаковые активные и реактивные сопротивления (RA =RB = RC и ХA=ХВ=ХС), фазные токи iA, iB и iC будут равны по величине и сдвинуты от соответствующих фазных напряжений на равные углы.

В этом случае получаем симметричную систему токов, при которой токи iA, iB, iC будут сдвинуты по фазе друг относительно друга на угол 120°, а ток i0 в нулевом проводе в любой момент времени равен нулю (рис. 208,б).

Очевидно, что при равномерной нагрузке можно удалить нулевой провод и передавать электрическую энергию источника к приемнику по трем линейным проводам 1, 2 и 3 (рис. 209).

Рис. 209. Схема «звезда без нулевого провода»

Такая схема называется «звезда без нулевого провода». При трехпроводной системе передачи электрической энергии в каждое мгновение ток по одному (или двум) проводу проходит от источника трехфазного тока к приемнику, а по двум другим (или одному) протекает обратно от приемника к источнику (рис. 210).

Рис 210. Кривые изменения токов в линейных проводах (а) при трехпроводной системе и направление в них токов в различные моменты времени (б в, г)

Векторная диаграмма напряжений для схемы «звезда без нулевого провода» при равномерной нагрузке фаз будет такая же, как и для схемы «звезда с нулевым проводом» (см. рис. 207).

Такими же будут и соотношения между фазными и линейными токами и напряжениями:

Iл = IФ и Uл = √3 UФ

Следует отметить, что схема «звезда без нулевого провода» может быть применена только при равномерной нагрузке фаз. Практически это имеет место лишь при подключении к источникам трехфазного тока электрических двигателей, так как каждый трехфазный электродвигатель снабжен тремя одинаковыми обмотками, которые равномерно нагружают все три фазы.

При неравномерной нагрузке напряжения на отдельных фазах нагрузки будут различными. На некоторых фазах (с меньшим сопротивлением) напряжение уменьшится, а на других увеличится по сравнению с нормальным, что является недопустимым.

Практически неравномерная нагрузка фаз возникает при питании трехфазным током электрических ламп, так как в этом случае распределение тока между всеми тремя фазами не может быть гарантировано (отдельные лампы могут включаться и выключаться в индивидуальном порядке). Особенно опасны в схеме «звезда без нулевого провода» обрыв или короткое замыкание в одной из фаз.

Можно показать путем построения соответствующих векторных диаграмм, что при обрыве в одной из фаз напряжение в других двух фазах уменьшается до половины линейного, вследствие чего лампы, включенные в эти фазы, будут гореть с недокалом.

При коротком замыкании в одной из фаз напряжение в других фазах увеличивается до линейного, т. е. в √З раз, и все лампы, включенные в этих фазах, перегорят. Поэтому при схеме «звезда с нулевым проводом» во избежание разрыва цепи нулевого провода в ней не устанавливают предохранители и выключатели.

Рисование фигур с помощью инструментов группы «Фигура» в Photoshop

Руководство пользователя Отмена

Поиск

Последнее обновление Jun 21, 2022 03:26:37 PM GMT

  1. Руководство пользователя Photoshop
  2. Введение в Photoshop
    1. Мечтайте об этом. Сделайте это.
    2. Новые возможности Photoshop
    3. Редактирование первой фотографии
    4. Создание документов
    5. Photoshop | Часто задаваемые вопросы
    6. Системные требования Photoshop
    7. Перенос наборов настроек, операций и настроек
    8. Знакомство с Photoshop
  3. Photoshop и другие продукты и услуги Adobe
    1. Работа с графическим объектом Illustrator в Photoshop
    2. Работа с файлами Photoshop в InDesign
    3. Материалы Substance 3D для Photoshop
    4. Photoshop и Adobe Stock
    5. Работа со встроенным расширением Capture в Photoshop
    6. Библиотеки Creative Cloud Libraries
    7. Библиотеки Creative Cloud в Photoshop
    8. Работа в Photoshop с использованием Touch Bar
    9. Сетка и направляющие
    10. Создание операций
    11. Отмена и история операций
  4. Photoshop на iPad
    1. Photoshop на iPad | Общие вопросы
    2. Знакомство с рабочей средой
    3. Системные требования | Photoshop на iPad
    4. Создание, открытие и экспорт документов
    5. Добавление фотографий
    6. Работа со слоями
    7. Рисование и раскрашивание кистями
    8. Выделение участков и добавление масок
    9. Ретуширование композиций
    10. Работа с корректирующими слоями
    11. Настройка тональности композиции с помощью слоя «Кривые»
    12. Применение операций трансформирования
    13. Обрезка и поворот композиций
    14. Поворот, панорамирование, масштабирование и восстановление холста
    15. Работа с текстовыми слоями
    16. Работа с Photoshop и Lightroom
    17. Получение отсутствующих шрифтов в Photoshop на iPad
    18. Японский текст в Photoshop на iPad
    19. Управление параметрами приложения
    20. Сенсорные ярлыки и жесты
    21. Комбинации клавиш
    22. Изменение размера изображения
    23. Прямая трансляция творческого процесса в Photoshop на iPad
    24. Исправление недостатков с помощью восстанавливающей кисти
    25. Создание кистей в Capture и их использование в Photoshop
    26. Работа с файлами Camera Raw
    27. Создание и использование смарт-объектов
    28. Коррекция экспозиции изображений с помощью инструментов «Осветлитель» и «Затемнитель»
  5. Бета-версия веб-приложения Photoshop
    1. Часто задаваемые вопросы | Бета-версия веб-приложения Photoshop 
    2. Общие сведения о рабочей среде
    3. Системные требования | Бета-версия веб-приложения Photoshop
    4. Комбинации клавиш | Бета-версия веб-приложения Photoshop
    5. Поддерживаемые форматы файлов | Бета-вервия веб-приложения Photoshop
    6. Открытие облачных документов и работа с ними
    7. Совместная работа с заинтересованными сторонами
    8. Ограниченные возможности редактирования облачных документов
  6. Облачные документы
    1. Облачные документы Photoshop | Часто задаваемые вопросы
    2. Облачные документы Photoshop | Вопросы о рабочем процессе
    3. Работа с облачными документами и управление ими в Photoshop
    4. Обновление облачного хранилища для Photoshop
    5. Не удается создать или сохранить облачный документ
    6. Устранение ошибок с облачными документами Photoshop
    7. Сбор журналов синхронизации облачных документов
    8. Общий доступ к облачным документам и их редактирование
    9. Общий доступ к файлам и комментирование в приложении
  7. Рабочая среда
    1. Основные сведения о рабочей среде
    2. Более быстрое обучение благодаря панели «Новые возможности» в Photoshop
    3. Создание документов
    4. Работа в Photoshop с использованием Touch Bar
    5. Галерея инструментов
    6. Установки производительности
    7. Использование инструментов
    8. Сенсорные жесты
    9. Возможности работы с сенсорными жестами и настраиваемые рабочие среды
    10. Обзорные версии технологии
    11. Метаданные и комментарии
    12. Комбинации клавиш по умолчанию
    13. Возможности работы с сенсорными жестами и настраиваемые рабочие среды
    14. Помещение изображений Photoshop в другие приложения
    15. Установки
    16. Комбинации клавиш по умолчанию
    17. Линейки
    18. Отображение или скрытие непечатных вспомогательных элементов
    19. Указание колонок для изображения
    20. Отмена и история операций
    21. Панели и меню
    22. Помещение файлов
    23. Позиционирование элементов с привязкой
    24. Позиционирование с помощью инструмента «Линейка»
    25. Наборы настроек
    26. Настройка комбинаций клавиш
    27. Сетка и направляющие
  8. Разработка содержимого для Интернета, экрана и приложений
    1. Photoshop для дизайна
    2. Монтажные области
    3. Просмотр на устройстве
    4. Копирование CSS из слоев
    5. Разделение веб-страниц на фрагменты
    6. Параметры HTML для фрагментов
    7. Изменение компоновки фрагментов
    8. Работа с веб-графикой
    9. Создание веб-фотогалерей
  9. Основные сведения об изображениях и работе с цветом
    1. Изменение размера изображений
    2. Работа с растровыми и векторными изображениями
    3. Размер и разрешение изображения
    4. Импорт изображений из камер и сканеров
    5. Создание, открытие и импорт изображений
    6. Просмотр изображений
    7. Ошибка «Недопустимый маркер JPEG» | Открытие изображений
    8. Просмотр нескольких изображений
    9. Настройка палитр цветов и образцов цвета
    10. HDR-изображения
    11. Подбор цветов на изображении
    12. Преобразование между цветовыми режимами
    13. Цветовые режимы
    14. Стирание фрагментов изображения
    15. Режимы наложения
    16. Выбор цветов
    17. Внесение изменений в таблицы индексированных цветов
    18. Информация об изображениях
    19. Фильтры искажения недоступны
    20. Сведения о цвете
    21. Цветные и монохромные коррекции с помощью каналов
    22. Выбор цветов на панелях «Цвет» и «Образцы»
    23. Образец
    24. Цветовой режим (или режим изображения)
    25. Цветовой оттенок
    26. Добавление изменения цветового режима в операцию
    27. Добавление образцов из CSS- и SVG-файлов HTML
    28. Битовая глубина и установки
  10. Слои
    1. Основные сведения о слоях
    2. Обратимое редактирование
    3. Создание слоев и групп и управление ими
    4. Выделение, группировка и связывание слоев
    5. Помещение изображений в кадры
    6. Непрозрачность и наложение слоев
    7. Слои-маски
    8. Применение смарт-фильтров
    9. Композиции слоев
    10. Перемещение, упорядочение и блокировка слоев
    11. Маскирование слоев при помощи векторных масок
    12. Управление слоями и группами
    13. Эффекты и стили слоев
    14. Редактирование слоев-масок
    15. Извлечение ресурсов
    16. Отображение слоев с помощью обтравочных масок
    17. Формирование графических ресурсов из слоев
    18. Работа со смарт-объектами
    19. Режимы наложения
    20. Объединение нескольких фрагментов в одно изображение
    21. Объединение изображений с помощью функции «Автоналожение слоев»
    22. Выравнивание и распределение слоев
    23. Копирование CSS из слоев
    24. Загрузка выделенных областей на основе границ слоя или слоя-маски
    25. Просвечивание для отображения содержимого других слоев
    26. Слой
    27. Сведение
    28. Совмещенные изображения
    29. Фон
  11. Выделения
    1. Рабочая среда «Выделение и маска»
    2. Быстрое выделение областей
    3. Начало работы с выделениями
    4. Выделение при помощи группы инструментов «Область»
    5. Выделение при помощи инструментов группы «Лассо»
    6. Выбор цветового диапазона в изображении
    7. Настройка выделения пикселей
    8. Преобразование между контурами и границами выделенной области
    9. Основы работы с каналами
    10. Перемещение, копирование и удаление выделенных пикселей
    11. Создание временной быстрой маски
    12. Сохранение выделенных областей и масок альфа-каналов
    13. Выбор областей фокусировки в изображении
    14. Дублирование, разделение и объединение каналов
    15. Вычисление каналов
    16. Выделение
    17. Ограничительная рамка
  12. Коррекции изображений
    1. Деформация перспективы
    2. Уменьшение размытия в результате движения камеры
    3. Примеры использования инструмента «Восстанавливающая кисть»
    4. Экспорт таблиц поиска цвета
    5. Корректировка резкости и размытия изображения
    6. Общие сведения о цветокоррекции
    7. Применение настройки «Яркость/Контрастность»
    8. Коррекция деталей в тенях и на светлых участках
    9. Корректировка «Уровни»
    10. Коррекция тона и насыщенности
    11. Коррекция сочности
    12. Настройка насыщенности цвета в областях изображения
    13. Быстрая коррекция тона
    14. Применение специальных цветовых эффектов к изображениям
    15. Улучшение изображения при помощи корректировки цветового баланса
    16. HDR-изображения
    17. Просмотр гистограмм и значений пикселей
    18. Подбор цветов на изображении
    19. Кадрирование и выпрямление фотографий
    20. Преобразование цветного изображения в черно-белое
    21. Корректирующие слои и слои-заливки
    22. Корректировка «Кривые»
    23. Режимы наложения
    24. Целевая подготовка изображений для печатной машины
    25. Коррекция цвета и тона с помощью пипеток «Уровни» и «Кривые»
    26. Коррекция экспозиции и тонирования HDR
    27. Фильтр
    28. Размытие
    29. Осветление или затемнение областей изображения
    30. Избирательная корректировка цвета
    31. Замена цветов объекта
  13. Adobe Camera Raw
    1. Системные требования Camera Raw
    2. Новые возможности Camera Raw
    3. Введение в Camera Raw
    4. Создание панорам
    5. Поддерживаемые объективы
    6. Виньетирование, зернистость и удаление дымки в Camera Raw
    7. Комбинации клавиш по умолчанию
    8. Автоматическая коррекция перспективы в Camera Raw
    9. Обратимое редактирование в Camera Raw
    10. Инструмент «Радиальный фильтр» в Camera Raw
    11. Управление настройками Camera Raw
    12. Обработка, сохранение и открытие изображений в Camera Raw
    13. Совершенствование изображений с улучшенным инструментом «Удаление точек» в Camera Raw
    14. Поворот, обрезка и изменение изображений
    15. Корректировка цветопередачи в Camera Raw
    16. Краткий обзор функций | Adobe Camera Raw | Выпуски за 2018 г.
    17. Обзор новых возможностей
    18. Версии обработки в Camera Raw
    19. Внесение локальных корректировок в Camera Raw
  14. Исправление и восстановление изображений
    1. Удаление объектов с фотографий с помощью функции «Заливка с учетом содержимого»
    2. Заплатка и перемещение с учетом содержимого
    3. Ретуширование и исправление фотографий
    4. Коррекция искажений изображения и шума
    5. Основные этапы устранения неполадок для решения большинства проблем
  15. Преобразование изображений
    1. Трансформирование объектов
    2. Настройка кадрирования, поворотов и холста
    3. Кадрирование и выпрямление фотографий
    4. Создание и редактирование панорамных изображений
    5. Деформация изображений, фигур и контуров
    6. Перспектива
    7. Использование фильтра «Пластика»
    8. Масштаб с учетом содержимого
    9. Трансформирование изображений, фигур и контуров
    10. Деформация
    11. Трансформирование
    12. Панорама
  16. Рисование и живопись
    1. Рисование симметричных орнаментов
    2. Варианты рисования прямоугольника и изменения обводки
    3. Сведения о рисовании
    4. Рисование и редактирование фигур
    5. Инструменты рисования красками
    6. Создание и изменение кистей
    7. Режимы наложения
    8. Добавление цвета в контуры
    9. Редактирование контуров
    10. Рисование с помощью микс-кисти
    11. Наборы настроек кистей
    12. Градиенты
    13. Градиентная интерполяция
    14. Заливка и обводка выделенных областей, слоев и контуров
    15. Рисование с помощью группы инструментов «Перо»
    16. Создание узоров
    17. Создание узора с помощью фильтра «Конструктор узоров»
    18. Управление контурами
    19. Управление библиотеками узоров и наборами настроек
    20. Рисование при помощи графического планшета
    21. Создание текстурированных кистей
    22. Добавление динамических элементов к кистям
    23. Градиент
    24. Рисование стилизованных обводок с помощью архивной художественной кисти
    25. Рисование с помощью узора
    26. Синхронизация наборов настроек на нескольких устройствах
  17. Текст
    1. Добавление и редактирование текста
    2. Универсальный текстовый редактор
    3. Работа со шрифтами OpenType SVG
    4. Форматирование символов
    5. Форматирование абзацев
    6. Создание эффектов текста
    7. Редактирование текста
    8. Интерлиньяж и межбуквенные интервалы
    9. Шрифт для арабского языка и иврита
    10. Шрифты
    11. Поиск и устранение неполадок, связанных со шрифтами
    12. Азиатский текст
    13. Создание текста
    14. Ошибка Text Engine при использовании инструмента «Текст» в Photoshop | Windows 8
  18. Видео и анимация
    1. Видеомонтаж в Photoshop
    2. Редактирование слоев видео и анимации
    3. Общие сведения о видео и анимации
    4. Предварительный просмотр видео и анимации
    5. Рисование кадров в видеослоях
    6. Импорт видеофайлов и последовательностей изображений
    7. Создание анимации кадров
    8. 3D-анимация Creative Cloud (предварительная версия)
    9. Создание анимаций по временной шкале
    10. Создание изображений для видео
  19. Фильтры и эффекты
    1. Использование фильтра «Пластика»
    2. Использование эффектов группы «Галерея размытия»
    3. Основные сведения о фильтрах
    4. Справочник по эффектам фильтров
    5. Добавление эффектов освещения
    6. Использование фильтра «Адаптивный широкий угол»
    7. Фильтр «Масляная краска»
    8. Эффекты и стили слоев
    9. Применение определенных фильтров
    10. Растушевка областей изображения
  20. Сохранение и экспорт
    1. Сохранение файлов в Photoshop
    2. Экспорт файлов в Photoshop
    3. Поддерживаемые форматы файлов
    4. Сохранение файлов в других графических форматах
    5. Перемещение проектов между Photoshop и Illustrator
    6. Сохранение и экспорт видео и анимации
    7. Сохранение файлов PDF
    8. Защита авторских прав Digimarc
  21. Печать
    1. Печать 3D-объектов
    2. Печать через Photoshop
    3. Печать и управление цветом
    4. Контрольные листы и PDF-презентации
    5. Печать фотографий в новом макете раскладки изображений
    6. Печать плашечных цветов
    7. Дуплексы
    8. Печать изображений на печатной машине
    9. Улучшение цветной печати в Photoshop
    10. Устранение неполадок при печати | Photoshop
  22. Автоматизация
    1. Создание операций
    2. Создание изображений, управляемых данными
    3. Сценарии
    4. Обработка пакета файлов
    5. Воспроизведение операций и управление ими
    6. Добавление условных операций
    7. Сведения об операциях и панели «Операции»
    8. Запись инструментов в операциях
    9. Добавление изменения цветового режима в операцию
    10. Набор средств разработки пользовательского интерфейса Photoshop для внешних модулей и сценариев
  23. Управление цветом
    1. Основные сведения об управлении цветом
    2. Обеспечение точной цветопередачи
    3. Настройки цвета
    4. Работа с цветовыми профилями
    5. Управление цветом документов для просмотра в Интернете
    6. Управление цветом при печати документов
    7. Управление цветом импортированных изображений
    8. Выполнение цветопробы
  24. Подлинность контента
    1. Подробнее об учетных данных для содержимого
    2. Идентичность и происхождение токенов NFT
    3. Подключение учетных записей для творческой атрибуции
  25. 3D-объекты и технические изображения
    1. 3D в Photoshop | Распространенные вопросы об упраздненных 3D-функциях
    2. 3D-анимация Creative Cloud (предварительная версия)
    3. Печать 3D-объектов
    4. 3D-рисование
    5. Усовершенствование панели «3D» | Photoshop
    6. Основные понятия и инструменты для работы с 3D-графикой
    7. Рендеринг и сохранение 3D-объектов
    8. Создание 3D-объектов и анимаций
    9. Стеки изображений
    10. Процесс работы с 3D-графикой
    11. Измерения
    12. Файлы формата DICOM
    13. Photoshop и MATLAB
    14. Подсчет объектов на изображении
    15. Объединение и преобразование 3D-объектов
    16. Редактирование 3D-текстур
    17. Коррекция экспозиции и тонирования HDR
    18. Настройки панели «3D»

Научитесь создавать фигуры на холсте и использовать функцию «Свойства интерактивной формы» для взаимодействия с фигурами.

В Photoshop предусмотрена удобная функция рисования и редактирования векторных фигур. Также можно преобразовать векторную фигуру в растровую или пиксельную. Прочитайте полную статью, чтобы узнать больше.

  • Создание фигур
  • Рисование произвольной фигуры
  • Доступ к устаревшим пользовательским фигурам
  • Заливка и обводка фигур
  • Рисование звезды с помощью инструмента «Многоугольник»

Выполните эти быстрые действия для создания фигур в Photoshop:

  1. Выберите инструмент «Фигура»

    На панели инструментов, нажмите и удерживайте значок группы инструментов Фигура (), чтобы вызвать различные варианты инструмента «Фигура» — Прямоугольник, Эллипс, Треугольник, Многоугольник, Линия и Произвольная фигура. Выберите инструмент для рисования нужной фигуры.

  2. Настройка параметров инструментов группы «Фигура»

    На панели параметров инструментов группы «Фигура» можно задать следующие настройки:

    • Режим: задайте режим для инструмента «Фигура» — Фигура, Контур и Пиксели.
    • Заливка: выберите цвет заливки фигуры.
    • Обводка: выберите цвет, ширину и тип обводки фигуры.
    • Ш и В: вручную задайте ширину и высоту фигуры.
    • Операции с контуром: используйте операции с контуром для настройки взаимодействия фигур друг с другом.
    • Выравнивание контура: используйте этот параметр для выравнивания и распределения компонентов фигуры.
    • Упорядочение контура: используйте этот параметр для настройки порядка расположения создаваемых фигур.
    • Дополнительные параметры фигур и контуров: щелкните значок шестеренки () для доступа к дополнительным параметрам фигур и контуров, чтобы задать такие атрибуты, как ширина и цвет отображаемого на экране контура, и параметры соблюдения пропорций при рисовании фигур.

  3. Рисование фигуры

    Чтобы нарисовать фигуру, выберите нужный инструмент группы «Фигура», затем щелкните кнопку мыши и перетащите указатель мыши на холсте. При этом автоматически создается новый слой-фигура на панели «Слои».

    • Удерживайте клавишу Shift во время рисования, чтобы сделать фигуры пропорциональными.
    • Выбрав слой-фигуру, используйте инструмент Перемещение, чтобы перемещать фигуру и менять ее расположение на холсте.
    • Чтобы легко масштабировать, трансформировать или поворачивать фигуру, выберите Редактирование > Свободное трансформирование или нажмите клавиши Control+T (Win) / Command+T (Mac).

  4. Редактирование свойств фигуры

    Можно легко редактировать свойства фигуры прямо с помощью элементов управления на холсте или с помощью раздела Свойства фигуры на панели Свойства. Элементы управления на холсте позволяют взаимодействовать с фигурами на более интуитивном уровне.

    Можно использовать элементы управления трансформированием и скруглением на холсте для коррекции внешнего вида фигуры. Модификаторы клавиатуры будут управлять трансформированием на холсте так же, как при использовании инструмента Трансформирование в Photoshop. Можно изменять радиус всех углов прямоугольника одновременно: удерживайте клавишу Alt (Win) или Option (Mac) во время перетаскивания для изменения радиуса одного угла. У треугольников изменяются все углы, даже если перетащить только один из них. С легкостью поворачивайте фигуру с помощью маркера поворота на холсте, который появляется при наведении курсора мыши на фигуру.

    Щелкните значок сброса () на панели «Свойства», чтобы сбросить сразу все изменения.

    Нарисуйте фигуру и используйте элементы управления на холсте, чтобы легко редактировать ее свойства.

    Нарисовав фигуру, можно щелкнуть любую точку холста, чтобы вызвать всплывающее диалоговое окно Создание фигуры и изменить параметры фигуры.

Выполните эти быстрые действия для заливки и обводки фигур: 

  1. На панели Слои выберите слой-фигуру, который необходимо залить или обвести.

  2. Для выбора типа заливки или обводки фигуры выполните одно из следующих действий.

    • Выберите любой инструмент группы «Фигура» (нажмите «U») из панели инструментов. На панели параметров инструментов выберите Заливка или Обводка.
    • На панели Свойства щелкните нужный тип заливки или обводки.  

  3. Во всплывающем меню выберите вариант заливки или обводки: Чистый цвет, Градиент или Узор.

    Чистый цвет: заполняет или обводит слой-фигуру текущим основным цветом. Для выбора другого цвета используйте палитру цветов или стили цвета.

    Градиент: для отображения диалогового окна «Редактор градиентов» выберите стиль градиента или щелкните градиент. Настройте дополнительные параметры градиента.

    • Значение параметра «Угол» определяет угол, под которым будет накладываться градиент.
    • Параметр «Инверсия» изменяет ориентацию цветов градиента.
    • Форма градиента определяется стилем.
    • Параметр «Масштаб» изменяет размер градиента.
    • Параметр «Выровнять по слою» использует ограничительную рамку слоя для расчета заполнения градиентом. Можно перетащить ее в окне изображения, чтобы переместить центр градиента.

    Узор: выберите узор в раскрывающемся меню и задайте дополнительные параметры.

    • Значение параметра «Угол» определяет угол, под которым будет накладываться узор. В средстве выбора угла можно указать определенный угол или вручную ввести нужную величину.
    • Параметр «Масштаб» задает размер узора. Введите значение в текстовое поле или с помощью ползунка.

Улучшение в выпуске Photoshop на компьютере за февраль 2021 года (22.2).

Рисовать произвольные фигуры можно, выбрав фигуры в раскрывающейся панели «Произвольная фигура». Можно также сохранить фигуру или контур и использовать их в дальнейшем как произвольную фигуру.

  1. Выберите инструмент Произвольная фигура в группе инструментов «Фигура» на панели инструментов.

  2. Чтобы просмотреть все произвольные фигуры, предусмотренные в Photoshop, щелкните значок шестеренки справа от палитры «Произвольная фигура» на панели параметров группы инструментов «Фигура». Появится список доступных фигур. Выберите любую произвольную фигуру на свое усмотрение.

  3. Если вы не нашли нужную фигуру, щелкните значок шестеренки на палитре «Произвольная фигура» и выберите Импорт фигур для импорта нужной фигуры из сохраненных файлов. Также можно создать и сохранить произвольную фигуру в своей библиотеке.

  4. Можно легко редактировать свойства инструмента «Произвольная фигура» прямо в разделе Свойства фигуры на панели Свойства. Кроме того, можно использовать элементы управления преобразованием на холсте для преобразования произвольной фигуры без изменения ее свойств. 

  5. Щелкните и перетащите в любом месте холста, чтобы нарисовать произвольную фигуру.

Улучшенная панель свойств для инструмента «Произвольная фигура»

Кроме того, набор параметров инструмента «Произвольная фигура» можно настроить прямо на панели Окна > Фигура. При выборе произвольной фигуры на панели Окна > Фигура этот набор также обновится на палитре Инструмент «Произвольная фигура» > Произвольная фигура.  

Доступ к свойствам можно получить только для произвольных фигур, нарисованных с помощью инструмента «Произвольная фигура». Для контура, преобразованного в фигуру, такой возможности нет. 

  1. Выберите контур на панели Контуры — векторную маску для слоя-фигуры, рабочий контур или сохраненный контур.

  2. Выберите меню Редактирование > Определить произвольную фигуру и введите имя для новой произвольной фигуры в диалоговом окне Имя фигуры. Новая фигура появится на всплывающей панели Фигура на панели параметров.

  3. Для сохранения новой произвольной фигуры в новой библиотеке выберите пункт Сохранить произвольные фигуры в меню раскрывающейся панели.

    Дополнительные сведения см. в разделе Работа со средством «Управление наборами».

Одна из основных фигур, которые мы учимся рисовать в детстве — пятиконечная звезда.

Выполните эти три простых действия, чтобы нарисовать звезду с помощью инструмента «Многоугольник».

  1. На панели инструментов щелкните и удерживайте значок группы инструментов «Фигура», чтобы вызвать различные варианты инструмента «Фигура». Выберите инструмент Многоугольник.

  2. Перетащите инструмент на холст, чтобы нарисовать многоугольник.

  3. Щелкните в любом месте холста, чтобы вызвать диалоговое окно Создание многоугольника и задайте следующие атрибуты.

    • Ширина и высота: вручную задайте ширину и высоту фигуры.
    • Симметричный: установите флажок для сохранения симметрии в многоугольнике.
    • Количество сторон: вручную введите желаемое количество сторон многоугольника. Например, задайте количество сторон до 5, если требуется нарисовать пятиконечную звезду.
    • Радиус скругления: вручную задайте радиус, чтобы получить скругленные углы у многоугольника.
    • Пропорции звезды: настройте процент пропорции, чтобы получить звезду идеальной формы.
    • Сглаживание внутренних углов звезды: установите флажок, чтобы скруглить внутренние углы звезды.
    • От центра: установите флажок, чтобы выровнять звезду от центра.
    Создание звезды с помощью инструмента «Многоугольник»

Если вы использовали устаревшие пользовательские фигуры из старых версий Photoshop и хотите добавить их в текущую версию, выполните следующие действия.

  1. В главном окне выберите Окно > Фигуры

  2. В правом верхнем углу панели «Фигуры» нажмите значок меню () и выберите Фигуры прежней версии и др.

Больше по теме

  • Сообщество Photoshop | Рисовать фигуры в Photoshop стало еще проще
  • Сообщество Photoshop | Краткие советы: как найти и использовать устаревшие фигуры в текущей версии Photoshop
  • Работа с инструментом «Линия»
  • Сведения о рисовании
  • Рисование с помощью инструмента «Перо»
  • Добавление векторных фигур в дизайны | Учебное пособие

 

Вход в учетную запись

Войти

Управление учетной записью

Как морские звезды обретают свою симметрию

В статье, опубликованной 4 ноября в журнале Current Biology, Зак Шварц, исследователь с докторской степенью в Институте Уайтхеда, вместе с исследователями в лаборатории члена Института Уайтхеда Иэном Чизманом и сотрудниками Массачусетского института Технологического института (MIT), Университета Майами и Курс эмбриологии Морской биологической лаборатории исследуют происхождение начальной полярности в первой клетке животного, которая устанавливает ось симметрии для развивающегося организма и лежит в основе первых шагов развития. Их исследование показывает, как специфический белок, называемый Dishavelled, локализуется в клетке, помогая создать эту полярность.

Все многоклеточные организмы начинаются с одной клетки — ооцита, клетки-предшественницы яйцеклетки, — которая несет в себе «план» для полностью развитого сложного существа, которым она станет. «Как создается этот многофункциональный план тела — один из самых глубоких вопросов в биологии развития», — сказал Шварц.

«Морские звезды и огромное разнообразие других животных имеют невероятно сложный план тела, ни один из которых невозможен без полярности исходной клетки», — сказал Чизман. «Эта работа показывает, как полярность возникает уже в мейотических делениях в развивающемся ооците с помощью неожиданной стратегии нарушения его симметрии и достижения асимметричного распределения факторов развития».

Чтобы изучить сложный процесс формирования тела, исследователи лаборатории Чизмана использовали тип морской звезды, называемый звездой летучей мыши, или Patiria miniata. Эти красочные животные радиально-симметричны во взрослом состоянии — у них обычно пять рук, иногда больше — но в личинках они билатерально-симметричны, как люди.

Зеркальная симметрия личинок морских звезд устанавливается, когда они являются яйцеклетками, называемыми ооцитами. Ключевым шагом в развитии этой организации является белок под названием Dishavelled, локализующийся на вегетативном или «нижнем» конце ооцита (который будет определять задний конец эмбриона), когда клетка готовится к делению на две дочерние клетки. клетки.

Растрепанные — названы так потому, что мутация в гомологичном белке у плодовых мушек придает их крошечным волоскам беспорядочный, взлохмаченный вид — является компонентом общего сигнального пути, называемого путем Wnt, который встречается у многих существ во всем животном мире. Путь служит различным целям в клетках, от формирования паттерна тела до пролиферации клеток. «Путь Wnt эволюционно древний», — сказал Шварц. «Медузы используют это, морские звезды используют это, люди используют это, и я думаю, что это действительно очень важно».

У морских звезд этот путь обеспечивает связь между исходной асимметрией ооцита и полярностью образующегося эмбриона. Растрепанный служит посредником внутри клеток морской звезды, передавая внешние сигналы, которые затем передаются через молекулярный путь к ядрам клеток.

Исследователи использовали замедленную съемку, чтобы визуализировать, как Disheveled перемещается вокруг ооцита, когда клетка проходит через различные фазы своего развития. Когда ооцит морской звезды находился в неделящейся фазе, Disheveled можно было обнаружить равномерно распределенным небольшими скоплениями по всей цитоплазме.

Когда ооцит готовился к делению, взлохмаченные скопления растворялись, а затем снова образовывались на дне клетки в самой дальней точке от ядра. Это обеспечило четкое различие между двумя концами ооцита (см. видео ниже).

Видео: Взлохмаченный, показан пурпурным цветом, сначала распространяется по всей клетке. Когда ооцит начинает мейоз, сборки Disheveled разрушаются, а затем восстанавливаются на вегетативном конце ооцита, который будет определять заднюю часть эмбриона, перед делением.

Шварцу было любопытно, как именно белок локализуется на дне ооцита. Нужно было исследовать несколько вариантов транспорта белка, поэтому он начал систематически исключать их; белок не транспортировался цитоскелетом клетки («Вы можете думать о них как о маленьких железнодорожных путях», — сказал Шварц), он не поддерживался токами цитоплазмы и не отталкивался каким-либо фактором на «верху» ооцита.

В это время Шварц связался с двумя сотрудниками физического факультета Массачусетского технологического института, которые помогли разработать эксперименты для дальнейшего изучения поведения Disheveled в ооцитах. «Именно тогда мы начали рассматривать идею распада и повторной сборки, которая является своего рода изюминкой статьи», — сказал Шварц. «Вы можете думать об этом как о кристаллах соли, растворяющихся в воде — вместо того, чтобы брать предварительно собранную вещь и физически транспортировать ее вниз [на дно яйцеклетки], идея состоит в том, что эти взъерошенные сборки начинаются повсюду, растворяются в своих отдельные компоненты, а затем выборочно преобразуются в растительную область».

«Морские звезды и огромное разнообразие других животных имеют невероятно сложный план тела, ни один из которых невозможен без полярности исходной клетки».

Точный механизм этого распада и преобразования пока не ясен. Шварц смог показать, что реформация не может происходить в отсутствие другого белка пути Wnt, называемого Frizzled, но поскольку Frizzled не является исключительным для нижней части ооцита, это не единственное, что вызывает повторную сборку. 

В будущем Шварц планирует выяснить, формируются ли агрегаты Disheveled в четких структурах, или же они группируются вместе в виде капель, разделенных фазами, таких как молекулы РНК, изученные в лаборатории члена Института Уайтхеда Анкура Джейна, или белковые молекулы, участвующие в транскрипции. из лаборатории члена Института Уайтхеда Ричарда Янга. «Меня интересует более широкий состав этих структур», — добавил он. «Они содержат только Dishavelled или есть другие ингредиенты?»

Независимо от того, как формируются сборки, новая информация о локализации Disheveled проливает свет на ранее загадочный этап в том, как путь Wnt играет роль в раннем формировании паттерна тела у морских звезд.

«Поразительно, что локализация Disheveled, по-видимому, является важной особенностью пути Wnt у морских звезд, а также у отдаленно родственных позвоночных», — сказал Шварц. «Я чувствую, что способность активировать этот путь в отдельных частях раннего эмбриона, интерпретируя полярность, встроенную в ооцит, может быть действительно важной особенностью эволюции плана тела животного».

Пятилучесимметричные хрупкие звезды движутся двусторонне, как люди

Зачем возиться с поворотами или поворотами? Хрупкая звезда не вращается, как это делает большинство животных. Он просто назначает другую из своих пяти конечностей новой передней частью и продолжает двигаться вперед. Предоставлено: Генри Эстли/Университет Брауна

Определяя «фронт» для управления направлением, пятилучевые симметричные хрупкие звезды используют передвижение способом, который обычно совершают билатерально-симметричные животные.

У хрупких звезд и людей есть кое-что общее: они двигаются совершенно одинаково. Хотя хрупкие звезды не обладают двусторонней симметрией, как люди и многие другие животные, они придумали механизм, позволяющий выбирать любую из своих пяти конечностей для направления своего движения по морскому дну. Как будто каждая рука может быть передней частью существа, способной передвигаться и определять направление. Результаты опубликованы в Журнале экспериментальной биологии.

Похоже, что хрупкая звезда, скромная пятилапая невода морского дна, движется очень похоже на нас.

В ходе серии первых экспериментов биолог-эволюционист из Университета Брауна Генри Эстли обнаружил, что хрупкие звезды, несмотря на отсутствие мозга, движутся очень скоординированным образом, выбирая центральное плечо для определения направления, а затем назначая другие конечности для движения вперед. . Тем не менее, когда хрупкая звезда хочет изменить направление, она указывает новый фронт, а это означает, что она выбирает для движения новую центральную руку и две другие конечности. Хрупкие звезды придумали механизм, позволяющий выбирать любую из своих пяти конечностей в качестве центрального элемента управления, каждая из которых способна определять направление или вмешиваться, чтобы помочь ей двигаться.

Результаты опубликованы в Журнале экспериментальной биологии .

Многие животные, в том числе люди, двусторонне симметричны — их можно разделить на одинаковые половинки, проведя линию по центру. Напротив, хрупкие звезды пятилучесимметричны: существует пять различных способов разрезать их на одинаковые половинки. В то время как билатерально-симметричные организмы усовершенствовали передвижение, назначив «голову», которая указывает направление, а затем приказывает другим частям тела следовать их примеру, радиально-симметричные животные не имеют такого центрального управления направлением.

«Что сделали хрупкие звезды, так это поставили крест на работе, — сказал Астлей. «Несмотря на то, что их тела радиально симметричны, они могут определять фронт и в основном вести себя так, как если бы они были билатерально симметричными, и пользоваться преимуществами билатеральной симметрии».

«Для животного, у которого нет центрального мозга, они довольно примечательны», — сказал Эстли, единственный автор статьи.

Астлей решил изучить хрупкие звезды после того, как заметил, что их придатки действуют подобно телу змеи, способной скручиваться и разворачиваться практически под любым углом. Тем не менее, когда он наблюдал за движением хрупких звезд, он не мог понять, как координируются отдельные руки. «Это было слишком запутанно», — сказал аспирант четвертого курса кафедры экологии и эволюционной биологии. «Нет явного фронта. Есть пять рук, которые все движутся, и я пытаюсь следить за всеми пятью, пока двигался диск (центрального тела)».

Он решил присмотреться, чего, на удивление, не сделал ни один другой ученый. Во время поездки в Белиз в январе 2009 года во главе с профессором и заведующим кафедрой Марком Бертнессом Эстли швырнул толстых иглы офиокомы ( Ophiocoma echinata ) в надувной бассейн и снял их на видео. Животные были добровольными субъектами. «Они ненавидят, когда их выставляют напоказ, — сказал Эстли, — поэтому мы поместили их посреди этого песчаного участка, и они бы двигались».

Чтобы двигаться, хрупкие звезды обычно назначают одну руку передней, в зависимости от того, в каком направлении она стремится двигаться. По словам Эстли, рука по обе стороны от центральной руки начинает гребное движение, очень похожее на морскую черепаху. Вся последовательность движений занимает около двух секунд. «В целом они довольно медленные, — сказал Эстли.

Чтобы повернуться, хрупкая звезда выбирает новый центральный рычаг и сопутствующие гребные рычаги, чтобы двигаться дальше. «Если нам, животным, нужно повернуться, нам нужно не только изменить направление движения, но и повернуть наши тела», — объяснил Астлей. «С этими парнями это похоже на: «Вот это фронт. Мне не нужно вращать диск моего тела».

Как ни странно, хрупкая звезда также выбирает другой тип передвижения — который для билатеральных органов может показаться движением назад — примерно в четверти случаев, задокументировал Эстли. В этом движении животное сохраняет тот же перед, но теперь указывает не гребущие вперед конечности, чтобы двигать его. Тогда возникает вопрос, почему хрупкая звезда не определяет новый фронт и просто не движется вперед? «Очевидно, что что-то определяет это», — сказал Астлей. «Это может быть относительная сила стимула на руках».

Ссылка: «Передвижение, когда вы кругом: количественный анализ передвижения хрупкой звезды с тупыми иглами, Ophiocoma echinata », Генри К. Эстли, 1 июня 2012 г., Journal of Experimental Biology .
DOI: 10.1242/jeb.068460

Большое овальное кольцо с голубой звездой и сапфиром, симметричный цветок

Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.

Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.

  • Нажмите, чтобы увеличить

Star Seller

Star Sellers имеют выдающийся послужной список в обеспечении отличного обслуживания клиентов — они постоянно получают 5-звездочные отзывы, вовремя отгружают заказы и быстро отвечают на любые полученные сообщения.

| 3549 продаж |

5 из 5 звезд

€117,81

Загрузка

Включая НДС (где применимо), плюс доставка

Размер кольца

Выберите вариант 5 США 5 1/4 США 5 1/2 США 5 3/4 США 6 США 6 1/4 США 6 1/2 США 6 3/4 США 7 США 7 1/4 США 7 1/2 США 7 3/4 США 8 США 8 1/4 США 8 1/2 США 8 3/4 США 9НАС 9 1/4 США 9 1/2 США 9 3/4 США 10 долларов США

Выберите опцию

В наличии осталось всего 6

Исследуйте связанные категории и поиски

Внесен в список 26 сентября 2022 г.

98 избранных

Сообщить об этом элементе в Etsy

Выберите причину… С моим заказом возникла проблемаОн использует мою интеллектуальную собственность без разрешенияЯ не думаю, что это соответствует политике EtsyВыберите причину…

Первое, что вы должны сделать, это связаться с продавцом напрямую.

Если вы уже это сделали, ваш товар не прибыл или не соответствует описанию, вы можете сообщить об этом Etsy, открыв кейс.

Сообщить о проблеме с заказом

Мы очень серьезно относимся к вопросам интеллектуальной собственности, но многие из этих проблем могут быть решены непосредственно заинтересованными сторонами. Мы рекомендуем связаться с продавцом напрямую, чтобы уважительно поделиться своими проблемами.

Если вы хотите подать заявление о нарушении прав, вам необходимо выполнить процедуру, описанную в нашей Политике в отношении авторских прав и интеллектуальной собственности.

alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Back To Top